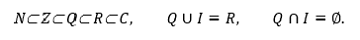Množiny čísel
Kľúčové slová:
množina, prvky, označenie množiny, konečná množina, nekonečná množina, prázdna množina, maximum, minimum, ohraničenie množiny, suprémum, infimum, okolie bodu, otvorený interval, uzavretý interval, polouzavretý interval sprava, polouzavretý interval zľava, vzťahy medzi množinami, operácie s množinami, základné číselné množiny, prirodzené čísla, celé čísla, racionálne čísla, iracionálne čísla, reálne čísla, absolútna hodnota reálnych čísel, komplexné čísla, vzťahy medzi základnými číselnými množinami
Množina je súhrn navzájom rozlíšiteľných objektov (prvkov), ktorý chápeme ako celok. Tieto jednotlivé prvky, ktoré sú súčasťou určitej množiny ju určujú. Číselné množiny sú také množiny, ktorých prvkami sú jedine čísla.
Množiny označujeme veľkými písmenami latinskej abecedy, pričom ich prvky sú značené malými písmenami. Skutočnosť, že nejaký prvok do istej množiny patrí označujeme symbolom ∈ a to, že do nej nepatrí zas symbolom ∉.Počet prvkov, ktorý množina obsahuje (ak je možné ho určiť) je vyjadrovaný zápisom:
|označenie množiny| = číselná hodnota.
Množinu je možné určiť dvojakým spôsobom:
- vymenovaním všetkých jej prvkov, napr.: A = {3, 6, 9};
- uvedením charakteristických vlastností prvkov, ktoré do nej patria, napr.: B = {x ∈ N, x < 10, 3 / x}.
Množina môže obsahovať:
- konečný počet prvkov - konečná množina;
- nekonečný počet prvkov - nekonečná množina;
- žiadny prvok - prázdna množina, označujeme ju symbolom ∅.
Každá neprázdna konečná množina má maximum a minimum. Číslo M považujeme za maximum množiny, vtedy keď máme množinu X, kde M je také číslo z X, že pre všetky x ∈ X platí x ≤ M. Takéto číslo označujeme ako maxX. Pričom m, je také číslo z množiny X, že pre všetky x ∈ X platí m ≤ x. Toto číslo m, nazývame minimum množiny a označujeme ho minX. Nekonečná množina čísel maximum a minimum mať nemusí.
Neprázdna číselná množina X sa nazýva:
- zhora ohraničená, ak existuje také číslo B, že pre každé x ∈ X platí x ≤ B, (B – horné ohraničenie množiny);
- zdola ohraničená, ak existuje také číslo b, že pre každé x ∈ X platí b ≤ x, (b – dolné ohraničenie množiny);
- ohraničená, ak je táto množina ohraničená zhora aj zdola;
- neohraničená, ak žiadne z predchádzajúcich tvrdení neplatí.
Najmenšie horné ohraničenie množiny X (v prípade, že existuje) sa nazýva suprémum množiny X a označujeme ho ako supX. Najväčšie dolné ohraničenie množiny X (pokiaľ existuje) sa nazýva infimum množiny X a zapisujeme ho ako infX. Vyznačujú sa týmito vlastnosťami:
- Pre každé x ∈ X platí supX ≥ x, infX ≤ x.
- Pre každé ε > 0 existujú čísla x1, x2 ∈ X, pre ktoré platí x1 ≥ supX - ε, x2 ≤ infX + ε.
- Ak je množina X ohraničená zhora, tak má suprémum. Ak je množina X ohraničená zdola, tak má infimum.
- Ak supX ∈ X, tak supX = maxX. Ak infX ∈ X, tak infX = minX.
Okolím čísla (bodu) a nazývame otvorený interval, ktorý obsahuje číslo a a označujeme ho:
Oε(a) = (a - ε, a + ε), pričom ε > 0.
Nech a, b sú ľubovoľné reálne čísla, medzi ktorými platí vzťah a < b. Potom môžeme vytvoriť množinu čísel:
- (a, b) = {x ∈ R: a< x < b} - otvorený interval, pre ktorý platí: a = inf(a, b), b = sup(a, b), minimum a maximum neexistuje;
- 〈a, b〉 = {x ∈ R: a ≤ x ≤ b} - uzavretý interval, pre ktorý platí: a = min〈a,b〉 = inf〈a, b〉, b = max〈a, b〉 = sup〈a, b〉;
- (a, b⟩ = {x ∈ R: a < x ≤ b} - polouzavretý interval sprava (zľava otvorený), pre ktorý platí: a = inf(a, b〉, b = max(a, b〉 = sup(a, b〉, minimum neexistuje;
- ⟨a, b) = {x ∈ R: a ≤ x < b} - polouzavretý interval zľava (sprava otvorený), pre ktorý platí: a = min⟨a, b) = inf⟨a, b), b = sup⟨a, b), maximum neexistuje.
Intervalmi nazývame aj množiny všetkých čísel x určených nerovnosťami:
- a ≤ x = ⟨a, ∞) - zľava uzavretý interval od a do nekonečna, pre ktorý platí: a = min⟨a, ∞) = inf⟨a, ∞), maximum a suprémum neexistuje;
- a < x = (a, ∞) - zľava otvorený interval od a do nekonečna, pre ktorý platí: a = inf(a, ∞), minimum, maximum a suprémum neexistuje;
- x ≤ b = (-∞, b⟩ – sprava uzavretý interval od mínus nekonečna po b, pre ktorý platí: b = max(-∞, b⟩ = sup(-∞, b⟩, minimum a infimum neexistuje;
- x < b = (-∞, b) – sprava otvorený interval od mínus nekonečna po b, pre ktorý platí: b = sup(-∞, b), maximum, minimum a infimum neexistuje;
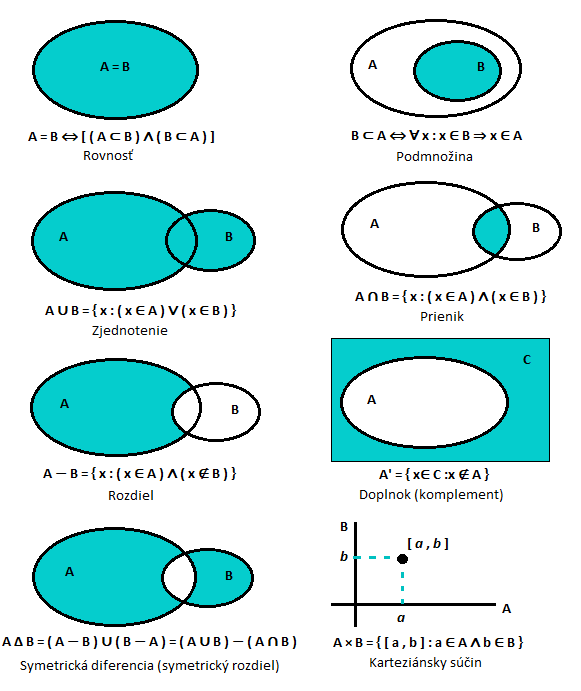
Medzi množinami môžu nastať rôzne vzťahy a taktiež s nimi môžeme vykonávať mnohé operácie, ktoré vieme znázorniť aj graficky:
Základné číselné množiny
N - Množina prirodzených čísel
Prirodzené čísla sú čísla, ktorými je udávaný počet prvkov množín. Patria sem kladné celé čísla/nezáporné celé čísla: 1,2,3,... . Niektoré zdroje považujú za prirodzené číslo aj 0. Súčtom a súčinom prirodzených čísel je možné získať len ďalšie prirodzené číslo.. Každé číslo n ∈ N je možné zapísať ako súčin prvočísel.
Prvočísla sú špeciálnym druhom prirodzených čísel. Sú to prirodzené čísla > 1, ktoré sú deliteľné iba 1 a sebou samým. Prvými prvočíslami sú čísla: 2, 3, 5, 7, 11, atď. Vzhľadom na ich unikátnosť našli veľké využitie najmä v kryptografii. Takmer všetky algoritmy určené na šifrovanie pracujú určitým spôsobom práve s prvočíslami.
Z - Množina celých čísel
Celé čísla sú všetky čísla, ktoré môžeme vyjadriť ako rozdiel dvoch prirodzených čísel. Ich súčtom, súčinom a rozdielom je celé číslo. Množinu celých čísel je možné získať rozšírením množiny N o záporné čísla. N je teda podmnožinou Z, čo matematicky vyjadrujeme zápisom N ⊂ Z.
Q - Množina racionálnych čísel
Racionálne čísla symbolizované písmenom Q (pre kvocient) sú čísla, ktoré je možné získať vydelením celých čísel navzájom alebo ich pomerom. Súčet, súčin, rozdiel a podiel racionálnych čísel (okrem delenia 0) je racionálne číslo. Akékoľvek racionálne číslo je možné zapísať ako zlomok, t. j. pomer celého čísla (čitateľa) a prirodzeného čísla (menovateľa). Vzhľadom na to, že každé celé číslo možno zapísať ako zlomok (konkrétne celé číslo delené 1), Z ⊂ Q.
I - Množina iracionálnych čísel
Iracionálne čísla sú čísla, ktoré možno vyjadriť v tvare nekonečného neperiodického desatinného zlomku. Napríklad: π, e, √2, sin 20°, log 7, ... . Ide o akékoľvek reálne číslo iné, ako racionálne. Z toho vyplýva, že Q ∩ I = ∅ a zároveň Q ∪ I = R.
R - Množina reálnych čísel
Množinu reálnych čísel tvorí zjednotenie racionálnych a iracionálnych čísel - Q ∪ I = R. Môžeme ju zapísať aj ako (-∞,∞). Množine reálnych čísel sú pripisované nasledovné vlastnosti:
-
usporiadaná - pre každé dve reálne čísla a, b platí práve jeden zo vzťahov: a = b, a < b, a > b;
-
hustá - medzi dvoma ľubovoľnými reálnymi číslami a, b, pre ktoré platí a < b, existuje aspoň jedno reálne číslo c tak, aby a < c < b;
-
uzavretá vzhľadom na operácie súčtu, súčinu, rozdielu a podielu - súčtom, súčinom, rozdielom a podielom reálnych čísel je reálne číslo;
-
je možné ju jednoznačne znázorniť na číselnej osi - každému reálnemu číslu možno priradiť jediný bod na číselnej osi a naopak;
-
ku každému reálnemu číslu existuje jeho absolútna hodnota.
Absolútna hodnota reálnych čísel
Absolútna hodnota reálneho čísla a sa označuje ako |a| a je definovaná ako:
|a| = a, ak a ≥ 0;
|a| = - a, ak a < 0.
Pre každé reálne číslo a platí:
- |a| = |-a|
- |a| ≥ a
- |a| = max{a, -a}
- |an| = |a|n, pre každé n ∈ N
- |a| = √a2
Pre každé dve reálne čísla a, b platí:
- |a . b| = |a| . |b|
- |a / b| = |a| / |b|, (b ≠ 0)
- |a + b| ≤ |a| + |b| (trojuholníková nerovnosť)
- |a| - |b| ≤ |a ± b| ≤ |a| + |b|
Geometrický význam absolútnej hodnoty reálneho čísla a je vzdialenosť obrazu čísla a na číselnej osi od jej začiatku. Vzdialenosť bodu a od bodu b na číselnej osi je preto vyjadrovaná ako |b - a|.
K reálnym číslam je dôležité poznamenať, že práca s nimi nie je úplne presná. Ani tie najvýkonnejšie počítače nedokážu pre všetky čísla získať ich hodnoty s celým desatinným rozvojom a počítať s nimi. To je dôvodom, prečo pri práci s reálnymi číslami často pracujeme iba s ich hodnotami zaokrúhlenými na určený počet desatinných miest.
C - Množina komplexných čísel
Komplexné čísla sú abstraktné, už nemerateľné veličiny, ktoré majú svoje vlastné aritmetické pravidlá a sú veľmi užitočné v rámci vedeckých výpočtov. Dôvodom ich zavedenia bola potreba určenia riešenia rovníc ako x2 + 1 = 0.
Všeobecne platí, že komplexné čísla rozširujú jednorozmerný svet reálnych čísel na dve dimenzie zahrnutím druhého, tzv. imaginárneho čísla. Komplexné číslo i, ktoré označuje imaginárnu jednotku, je definované ako (kladné) riešenie spomínanej rovnice x2 + 1 = 0 , alebo, inými slovami, i = √-1.
Pre imaginárne číslo i platí:
i2 = -1, i3 = - i, i4 = 1
Každé komplexné číslo je charakterizované dvojicou čísel (a, b), kde a je skutočná časť a b imaginárna časť čísla. V tomto zmysle možno komplexné číslo tiež vidieť geometricky, ako vektor v komplexnej rovine. Táto komplexná rovina je dvojrozmerný súradnicový systém, kde skutočná časť komplexného čísla označuje vzdialenosť od vertikálnej osi (alebo referenčnej čiary) a imaginárna časť označuje vzdialenosť od horizontálnej osi. Obe osi sa stretávajú vo svojom pôvode - v bode 0. Horizontálna os sa označuje aj ako reálna os a vertikálna os ako imaginárna os.
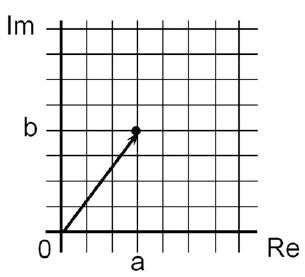
Komplexné číslo z sa tiež píše ako z = a + bi. Pri práci s komplexnými číslami a pri manipulácii s nimi je nutné si uvedomiť, že komplexné číslo môže byť reprezentované dvoma spôsobmi:
- ako dvojica alebo vektor (a,b) v dvojrozmernej komplexnej rovine;
- ako číslo a + bi.
Spomínané vzťahy, ktoré medzi základnými číselnými množinami platia je možné znázorniť pomocou nižšie uvedeného obrázka a vyjadriť zápisom:
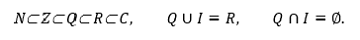

Úlohy
Príklad 1.
L je množina prirodzených čísel z intervalu ⟨2,5). Vypíšte jej prvky.
Riešenie v SageMath
Príklad 2.
M je konečná množina prirodzených čísel 2 + 5*j < 100. Aké čísla sú jej prvkami?
Riešenie v SageMath
Príklad 3.
Uveďte definíciu prirodzených čísel N (nekonečnej množiny).
Riešenie v SageMath
Príklad 4.
Definujte množinu prirodzených čísel N0 obsahujúcu aj číslo 0 (nekonečnú množinu).
Riešenie v SageMath
Príklad 5.
Zistite, či vybrané číslo (napr. 7) patrí do množiny N.
Riešenie v SageMath
Príklad 6.
Určte, či je dané číslo (napr. 2017) prvočíslo.
Riešenie v SageMath
Príklad 7.
Vypíšte a určte počet prvkov spomínanej množiny M.
Riešenie v SageMath
Príklad 8.
Napíšte, aký je počet prvkov nekonečnej množiny prirodzených čísel N.
Riešenie v SageMath
Príklad 9.
Vypíšte čísla z intervalu prirodzených čísel ⟨17, 31).
Riešenie v SageMath
Príklad 10.
Definuje množinu reálnych čísel R.
Riešenie v SageMath
Príklad 11.
Uveďte množinu reálnych čísel R - {0}.
Riešenie v SageMath
Príklad 12.
Zadajte interval reálnych čísel I = (-oo,1) + (4,+oo).
Riešenie v SageMath
Príklad 13.
Určte prienik dvoch množín. Napríklad množín I1 = 〈0,3〉 a I2 = 〈1,6〉.
Riešenie v SageMath
Príklad 14.
Určte zjednotenie dvoch množín. Znova napríklad množín I1 = 〈0,3〉 a I2 = 〈1,6〉.
Riešenie v SageMath
SageMath Cell