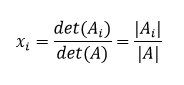Lineárna algebra
Kľúčové slová:
lineárna algebra, sústava lineárnych rovníc, matica sústavy, vektor pravých strán, vektor premenných, maticový tvar sústavy lineárnych rovníc, matica, veľkosť matice, druhy matíc, štvorcové matice, algebraické operácie s maticami, násobenie matice konštantou, súčet matíc, rozdiel matíc, súčin matíc, hodnosť matice, frobeniova veta, ekvivalentné matice, elementárne úpravy matíc, regulárne matice, inverzné matice, Gaussov tvar matice, Gaussova eliminačná metóda, predná eliminácia, spätná substitúcia, Gauss - Jordanova eliminačná metóda, determinanty, determinant a inverzná matica, vlastnosti determinantu, Cramerovo pravidlo
Lineárna algebra je jedným z najdôležitejších matematických a výpočtových nástrojov v rôznych vedných odboroch. Je ústrednou časťou čistej aj aplikovanej matematiky.
Lineárna algebra je matematickou disciplínou zaoberajúcou sa vektorovými priestormi, často konečných alebo spočítateľných nekonečných rozmerov, ale aj ich lineárnymi transformáciami. Zjednodušene povedané ide o oblasť matematiky zaoberajúcu sa vektormi, ktorým sme venovali svoju pozornosť už v časti Analytická geometria, a maticami.
Jadrom lineárnej algebry je problém riešenia sústavy lineárnych rovníc s viacerými neznámymi.
Sústava lineárnych rovníc
Lineárna rovnica s n premennými x1, x2, …, xn je akákoľvek rovnica tvaru
a1x1 + a2x2 + ⋯ + anxn = b
kde b, a1, a2, …, an (koeficienty) sú čísla patriace do množiny reálnych, prípadne komplexných čísel.
K nájdeniu úplného riešenia lineárnej rovnice čo i len s dvoma premennými sú potrebné minimálne dve nezávislé rovnice. Práve takáto množina lineárnych rovníc je najmenšou možnou sústavou lineárnych rovníc.
Všeobecne teda platí, že sústava lineárnych rovníc je množina dvoch alebo viacerých lineárnych rovníc s dvoma alebo viacerými premennými - neznámymi.
Sústava m lineárnych rovníc o n neznámych môže byť zapísaná ako

kde:
- aij sú koeficienty sústavy,
- xj sú premenné sústavy,
- bi sú absolútne členy sústavy,
- i = 1, 2 , ..., m a j = 1, 2, ..., n.
Sústavu lineárnych rovníc môžeme rozložiť v podobe matíc. Koeficienty sústavy lineárnych rovníc môžeme napísať ako maticu, nazývanú aj matica sústavy, ktorá má tvar

Absolútne členy sústavy tvoria tzv. vektor pravých strán, ktorý zapisujeme ako stĺpcovú maticu
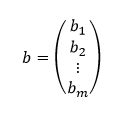
Vektor premenných má maticový tvar
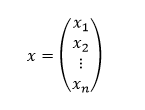
Celú sústavu lineárnych rovníc je teda možné zapísať ako
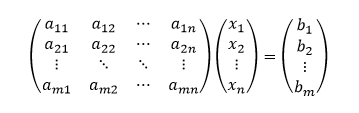
čo môžeme vyjadriť aj maticovým zápisom
Ax = b
K riešeniu sústavy rovníc sa tak dokážeme dostať vypočítaním výrazu
x = A-1b
Sústava lineárnych rovníc môže mať:
- práve jedno riešenie
- nekonečne veľa riešení
- žiadne riešenie
Matice
Matica je pole skalárov, resp. množina čísel alebo iných matematických objektov, ktoré sú jej prvkami. Veľkosť matice vyjadrujeme zápisom
m × n
pričom
- m určuje počet riadkov matice,
- n určuje počet stĺpcov matice.
Na základe hodnôt čísel m a n tak vieme určiť o aký druh matice sa jedná:
- ak máme maticu n × n (s rovnakým počtom riadkov a stĺpcov), hovoríme o štvorcovej matici;
- ak máme maticu m × n (s odlišným počtom riadkov a stĺpcov), hovoríme o obdĺžnikovej matici;
- ak máme maticu 1 × n, hovoríme o riadkovej matici;
- ak máme maticu m × 1, vravíme o stĺpcovej matici.
Štvorcová matica A = [ aij ]n×n môže byť:
- diagonálna, ak aij = 0, pričom i ≠ j;
- jednotková (označovaná In), ak aij = 0, pričom i ≠ j a aii = 1 pre 1 ≤ i ≤ n;
- nulová, ak každý jej prvok = 0;
- regulárna, ak je jej hodnosť rovná n;
- singulárna, ak jej hodnosť nie je rovná n;
- horná trojuholníková, ak aij = 0, pre i > j;
- dolná trojuholníková, ak aij = 0, pre i < j;
- symetrická, ak aij = aji.
Prvky aii nazývame diagonálne prvky. Prvok aij nazývame pivotom i-teho riadku, ak aik = 0 pre k < j, teda ak aij je prvým nenulovým prvkom i-teho riadku.
Algebraické operácie s maticami
Každá operácia s maticou je operáciou s každým jej prvkom. Medzi základné algebraické operácie s maticami patria vynásobenie matice konštantou, súčet matíc a súčin matíc.
Násobenie matice konštantou
Ak A = [ aij ]m x n je matica a c je konštanta, tak c-násobkom matice A je matica
c.A = [ c.aij ]m x n
Súčet matíc
Súčet matíc je možné definovať iba pre matice rovnakého rozmeru. Ak sú teda matica A = [ aij ]m x n a B = [ bij ]m x n maticami s rovnakým rozmerom m × n, tak ich súčtom je matica
C = A + B = [ cij ]m × n, pričom cij = aij + bij
Jednoducho povedané, pri súčte matíc sčítavame ich prvky na rovnakých miestach.
Rozdiel matíc
Rozdiel matíc sa riadi takým istým pravidlom, ako ich súčet. No namiesto sčítavania prvkov na rovnakých miestach ich navzájom odčítavame.
Súčin matíc
Pri súčine matíc na rozdiel od súčinu konštánt záleží na ich poradí, platí
AB ≠ BA
Maticu A možno sprava vynásobiť maticou B iba, ak n (počet stĺpcov) matice A sa rovná m (počtu riadkov) matice B. Platí, že ak A = [ aik ]m x l a B = [ bkj ]l x n sú matice rozmeru m x l a l x n, tak ich súčinom je matica
C = AB
typu m x n a jej i,j-ty prvok vypočítame pomocou vzťahu
cij = ai1.b1j + ai2.b2j + ⋯ + ail.blj
Hodnota [ i, j ]-tého prvku matice C = AB je teda skalárnym súčinom i-teho riadku matice A a j-tého stĺpca matice B.
Hodnosť matice a Frobeniova veta
Pod pojmom hodnosť matice rozumieme počet lineárne nezávislých riadkov danej matice. Ide o skalárnu hodnotu reprezentujúcu počet nenulových riadkov matice upravenej pomocou elementárnych úprav na trojuholníkový, resp. lichobežníkový tvar. Jej hodnota sa elementárnymi úpravami matice nemení.
Hodnosť matice A označujeme ako h(A).
Platí vzťah h(A) = h(AT) – hodnosť transponovanej matice sa rovná hodnosti pôvodnej matice. Transponovanou maticou matice A rozmeru m × n rozumieme maticu AT rozmeru n × m, ktorú získame zámenou riadkov a stĺpcov pôvodnej matice A.
Hodnotou hodnosti matice sústavy lineárnych rovníc dokážeme okrem iného určiť, koľko riešení daná sústava má a či je vôbec riešiteľná. Takéto poznanie nám prináša tzv. Frobeniova veta.
Frobeniova veta
Nech je definovaná sústava m lineárnych rovníc o n neznámych

ktorej maticový zápis je
Ax = b
Maticou sústavy nech je matica

a nech matica

je rozšírenou maticou matice sústavy o vektor pravých strán.
Potom môžeme povedať, že sústava Ax = b:
- má práve jedno riešenie, ak h(A) = h(A,b) = n;
- má nekonečne veľa riešení, ak h(A) = h(A,b) < n;
- nemá žiadne riešenie, ak h(A) ≠ h(A,b).
Frobeniova veta tak ponúka algoritmus na všeobecné riešenie sústavy lineárnych rovníc, ktorý pozostáva z troch krokov – výpočet hodnosti matice A, výpočet hodnosti rozšírenej matice (A,b) a následná aplikácia Frobeniovej vety.
Ekvivalentné matice
Nech matice A a B sú matice rovnakého rozmeru. Tieto matice nazývame ekvivalentné ak dokážeme maticu B získať z matice A pomocou jednej alebo kombináciou jej elementárnych úprav.
Elementárnymi úpravami matice A rozumieme operácie ako:
- zámena riadkov/stĺpcov matice,
- vynásobenie riadku/stĺpca matice nenulovou konštantou,
- pripočítanie násobku jedného riadku/stĺpca k inému.
Skutočnosť, že matice A a B, alebo akékoľvek iné matice sú navzájom ekvivalentné vyjadrujeme znakom ~. Zápis toho, že matice A a B sú ekvivalentné môže vyzerať aj takto: A ≅ B.
Regulárne matice
Okrem vyššie uvedenej charakteristiky regulárnych matíc, platí pre tento typ matíc ešte omnoho viac tvrdení.
Štvorcovú maticu A rozmeru n × n považujeme za regulárnu, ak:
- A ~ In,
- h(A) = n,
- det(A) ≠ 0,
- k matici A existuje inverzná matica.
Ak tieto tvrdenia neplatia, matica A je nazývaná singulárna matica.
Inverzné matice
K regulárnej matici A rozmeru n × n existuje inverzná matica A-1, ktorá je taktiež štvorcová, práve vtedy, keď
A-1.A = A.A1 = I
Rovnako, ako aj s ostatnými maticami aj s inverznými maticami je možné vykonávať rôzne algebrické operácie. K transponovaniu a súčinu inverzných matíc sú stanovené určité zásady.
Nech A a B sú štvorcové matice, ku ktorým existujú inverzné matice, potom platí:
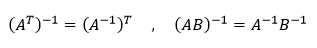
Význam určenia inverznej matice spočíva v pravidle, ktoré vraví, že matice nie je možné navzájom deliť. Násobením oboch strán výrazu inverznou maticou však dokážeme dosiahnuť to isté.
Sústavu lineárnych rovníc Ax = b môžeme teda vyriešiť tým, že vynásobíme rovnicu inverznou maticou:
A-1.A.x = I.x = x = A-1.b
Ako nám je známe z definície inverznej matice, vynásobením matice jej inverznou maticou získame jednotkovú maticu. Násobenie jednotkovou maticou je ekvivalentné k násobeniu výrazu číslom 1.
Nie vždy však existuje inverzná matica. Pokiaľ k matici A existuje inverzná matica, matici A vravíme, že je invertovateľná. Platí, že inverzná matica A-1 k matici A existuje iba ak determinant matice det(A) nie je rovný 0, čo vyplýva aj zo samotnej definície regulárnej matice.
Na určenie toho, či k istej matici existuje inverzná matica a dokonca aj k jej samotnému výpočtu je možné použiť nasledujúci pomerne jednoduchý algoritmus.
Majme regulárnu maticu A rozmeru n × n, z ktorej utvoríme maticu C typu n × 2n tým, že k n stĺpcom matice A priložíme rovnako veľkú jednotkovú maticu In. Symbolicky môžeme túto maticu C zapísať ako
![C = [ A | I_n ]](../img/vzorec_vypocet_inverznej_matice_krok1.png)
Maticu C upravíme pomocou elementárnych úprav na jej redukovaný Gaussov tvar, čím získame maticu, ktorú budeme označovať C´. Ak prvých n stĺpcov tejto matice tvorí jednotkovú maticu, tak zvyšných n stĺpcov tvorí inverznú maticu k pôvodnej matici A a platí:
![C´ = [ I_n | A^(-1) ]](../img/vzorec_vypocet_inverznej_matice_krok2.png)
Ak prvých n stĺpcov tejto matice nevytvára jednotkovú maticu, tak matica A nie je invertovateľná.
Gaussove eliminačné metódy
V lineárnej algebre a obzvlášť pri riešení sústavy lineárnych rovníc zohráva významnú úlohu Gaussova eliminačná metóda. K jej porozumeniu je však potrebné sa prv oboznámiť s viackrát spomínaným pojmom Gaussov tvar matice.
Gaussov tvar matice
Hovoríme, že matica je v Gaussovom tvare v prípade, že sú splnené tieto štyri podmienky:
- každý pivot = 1 (nazývame ho aj vedúca jednotka),
- každý prvok v stĺpci pod vedúcou jednotkou = 0,
- vedúca jednotka v každom riadku sa nachádza vpravo od vedúcich jednotiek všetkých vyššie položených riadkov,
- prípadné riadky obsahujúce iba nuly nasledujú ž za všetkými riadkami obsahujúcimi vedúce jednotky.
Okrem obyčajného Gaussovho tvaru poznáme aj redukovaný Gaussov tvar. O matici môžeme povedať, že je v redukovanom Gaussovom tvare v prípade, že okrem týchto 4 podmienok platí, že aj každý prvok v stĺpci nad vedúcou jednotkou je rovný 0.
Pre každú maticu existuje postupnost' riadkových operácií, pomocou ktorých je možné danú maticu upravit' tak, aby spĺňala vyššie uvedené podmienky, tzn., že každú maticu je možné upraviť do Gaussovho tvaru.
Gaussova eliminačná metóda
Cieľom Gaussovej eliminačnej metódy je prejsť od sústavy lineárnych rovníc Ax = b k ekvivalentnej sústave Cx = d pomocou riadkových operácií, pričom matica C má mať vlastnosti
cij = 0 pre i > j a cii ≠ 0
Sústavy lineárnych rovníc Ax = b a Cx = d považujeme za ekvivalentné, keď platí, že každé riešenie sústavy Ax = b je zároveň riešením sústavy Cx = d a naopak. Získaním riešenia sústavy Cx = d tak získame aj riešenie pôvodnej sústavy.
Riešenie sústavy lineárnych rovníc Gaussovou eliminačnou metódou pozostáva z dvoch hlavných fáz:
- predná eliminácia - úpravu sústavy, resp. matice na horný trojuholníkový tvar
- spätná substitúcia - hodnoty neznámych dopočítané z vytvorenej redukovanej trojuholníkovej matice
Úplne prvým krokom k získaniu riešenia sústavy lineárnych rovníc pomocou Gaussovej eliminačnej metódy je úprava tejto sústavy do tvaru rozšírenej matice. Hoc tento krok nie je povinný, je náramne nápomocný, keďže jediné s čím budeme vďaka nemu v prvej fáze pracovať sú čísla.
Predpokladajme, že poznáme sústavu lineárnych rovníc Ax = b alebo z nej vzniknutú maticu (A,b), ktorá je nenulová, t.j. má aspoň jeden nenulový prvok ars. Zámenou riadkov a stĺpcov vieme zaistiť, že týmto prvkom bude prvok a11 ≠ 0. Predná eliminácia následne pokračuje eliminovaním prvej neznámej vo všetkých okrem prvej rovnice, resp. vynulovaním prvkov nachádzajúcich sa pod spomínaným prvkom a11, tým, že pripočítame vhodný násobok prvého riadku matice (prvej rovnice) k ostatným.
Potom eliminujeme druhú neznámu vo všetkých rovniciach, resp. riadkoch, okrem prvých dvoch pripočítaním vhodného násobku druhej rovnice (riadku) ku každej ďalšej nachádzajúcej sa pod ňou.
Týmto spôsobom pokračujeme, až pokým nám z pôvodnej matice nevznikne horná trojuholníková alebo lichobežníková matica (C,d), ktorá je rozšírenou maticou sústavy spomínanej ekvivalentnej sústavy lineárnych rovníc Cx = d.
V prípade, že sme pracovali s maticami a nie so sústavou lineárnych rovníc, upravíme výslednú maticu do tvaru sústavy, ktorá môže vyzerať napr. takto:
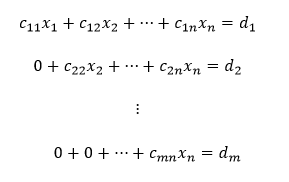
Následne prechádzame do druhej fázy tohto spôsobu riešenia sústavy lineárnych rovníc, v ktorej sa ekvivalentnými úpravami každej z nich a dosadzovaním zistených hodnôt neznámych postupne dopracujeme k celkovému riešeniu sústavy Cx = d, čím získavame taktiež riešenie pôvodnej sústavy Ax = b.
Gauss - Jordanova eliminačná metóda
Ďalším spôsobom riešenia sústavy lineárnych rovníc a z nich vzniknutých matíc je Gauss-Jordanova eliminačná metóda.
Táto metóda je v podstate len akousi rozvinutejšou verziou Gaussovej eliminačnej metódy. Jej cieľom totiž nie je upraviť maticu sústavy (maticu koeficientov) len do trojuholníkového, resp. lichobežníkového tvaru, ale až do redukovaného Gaussovho tvaru.
Riešenie sústavy lineárnych rovníc je tak možné zistiť hneď po úprave matice do požadovaného tvaru. Vytráca sa tak potreba spätnej substitúcie. Pravá strana výslednej rozšírenej matice je tvorená práve riešeniami danej sústavy.
Determinanty
Determinant je multilaterálnym zobrazením, ktoré každej štvorcovej matici priraďuje jednu skalárnu hodnotu – číslo. Determinant matice A zapisujeme ako det(A) alebo |A|.
Pre maticu A = ( a11 ) s rozmerom 1 × 1 platí det(A) = a11.
Pre maticu A rozmeru 2 × 2 môžeme vypočítať tzv. determinant druhého stupňa, pre ktorý platí
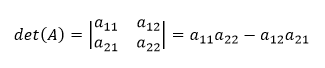
Determinant tretieho stupňa matice A, ktorej rozmer je 3 × 3 vyrátame ako
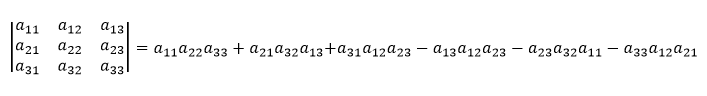
Determinant matice A s rozmerom 3 × 3 môžeme taktiež vypočítať využitím tzv. Sarrusovho pravidla.
Toto pravidlo vraví, že ak pridáme pod maticu A jej prvé dva riadky, alebo ak za maticu A pridáme prvé dva stĺpce tejto matice, tak kladnými zložkami determinantu sú trojice prvkov ležiacich na diagonálach sprava a zápornými zložkami sú tie trojice prvkov, ktoré ležia na diagonálach zľava.
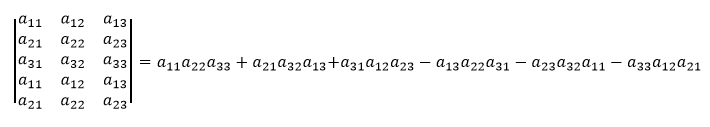
Sarrusovo pravidlo sa však pre štvorcové matice väčšieho rozmeru nedá zovšeobecniť. Vzniká tak potreba všeobecne definovať determinant n-tého stupňa.
Nech je daná matica A rozmeru n × n. Maticu, ktorá vzniká z A tým, že vynecháme jej i-ty riadok a j-ty stĺpec označujme ako maticu Aij. Potom determinant matice A môžeme definovať vzťahom
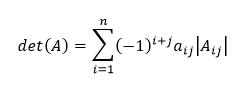
kde aij je prvok matice A, ktorý je v i-tom riadku a j-tom stĺpci. Determinant matice Aij nazývame aj subdeterminant prvku aij matice A.
Tento vzťah je definíciou determinantu pomocou tzv. rozvoja j-teho stĺpca. Pri výpočte tohto výrazu si tak musíme pevne zvoliť ľubovoľný stĺpec matice, resp. hodnotu j, ktorá je indexom matice A. V prípade, že by sme iterovali cez premenné j, vraveli by sme o rozvoji i-teho riadku a mali pevne zvolený riadok i matice A.
Daný výraz je možné zjednodušiť definovaním hodnoty algebrického doplnku prvku aij matice A vzťahom
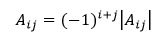
Potom môžeme determinant matice A rozmeru n × n definovať aj ako
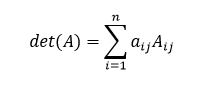
Determinant a inverzná matica
Determinant je okrem iného možné použiť aj k výpočtu už spomínanej inverznej matice. Pre výpočet inverznej matice k matici A platí vzťah
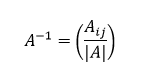
Podmienka existencie inverznej matice, ktorá vraví, že k matici A existuje inverzná matica A-1 iba ak det(A) ≠ 0 je udaním tohto vzorca jej výpočtu omnoho jasnejšia, keďže číslom 0 sa vo všeobecnosti nedelí.
Vlastnosti determinantu
Determinant je pojmom lineárnej algebry s viacerými vlastnosťami, ktoré dokážu výrazne ovplyvniť proces jeho výpočtu. Dôležitými vlastnosťami determinantu sú najmä tie, ktoré súvisia s elementárnymi úpravami vykonávanými na riadkoch, ale aj stĺpcoch matice, resp. sústavy.
Tieto vlastnosti znejú nasledovne:
- Ak B je matica, ktorá vznikne z matice A jednou aplikáciou prvej elementárnej operácie, tak
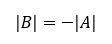
- Ak matica B vznikne z matice A pomocou druhej elementárnej operácie, čiže tak, že niektorý jej riadok je vynásobený konštantou c, tak
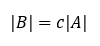
- Aplikáciou tretej elementárnej úpravy sa determinant matice nemení
- Ak je v matici A niektorý riadok/stĺpec násobkom iného riadku/stĺpca, čiže niektoré vektory tvoriace túto maticu sú lineárne závislé, potom aj celá táto sústava je lineárne závislá a
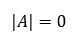
- Ak je matica A = [ aij ] n×n trojuholníková, tak jej determinant je rovný súčinu jej diagonálnych prvkov, takže
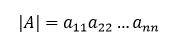
Úprava na Gaussov tvar je tak jednou z najjednoduchších metód výpočtu determinantu matice. Jej využitím je umožnený spomínaný výpočet determinantu ako súčinu diagonálnych prvkov výslednej trojuholníkovej matice, vynásobený znamienkom mínus pri každej zámene, ako vyplýva z prvej z uvedených vlastností determinantu alebo konštantou, čo vyplýva z jeho druhej vlastnosti. Pokiaľ nám úpravou na Gaussov tvar vznikne nulový riadok – nulový vektor, tak táto sústava je automaticky lineárne závislá a jej determinant je rovný 0, keďže nulový vektor je lineárnou kombináciou akéhokoľvek vektora.
Pomocou determinantov dokážeme taktiež získať riešenie sústavy lineárnych rovníc, keď det(A) ≠ 0. Takáto sústava lineárnych rovníc má práve jedno riešenie.
Cramerovo pravidlo
Cramerovo pravidlo je doslovnou formuláciou použitia determinantov k riešeniu sústavy lineárnych rovníc.
Nech je určená sústava n lineárnych rovníc o n neznámych
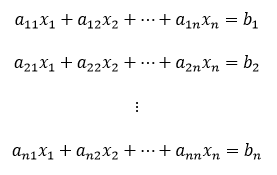
ktorej matica sústavy je označovaná A a det(A) ≠ 0, alebo rozvinuto zapísané

a nech det(Ai), alebo tiež |Ai| je determinantom matice vytvorenej z matice A nahradením jej i-teho stĺpca vektorom b, napríklad
.png)
Potom má sústava lineárnych rovníc jediné riešenie, ktoré je možné vyjadriť v tvare
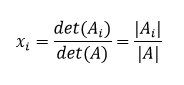
Cramerovo pravidlo je bohužiaľ pri väčších sústavách výpočtovo veľmi neefektívne a zdĺhavé, a v praxi sa teda tak často nepoužíva. Môžeme ho však využiť pri riešení jednoduchších úloh, kde n ∈ ⟨ 2,8 ), a iba ak je štvorcová matica tejto sústavy regulárna.
Úlohy
Príklad 1.
Riešte sústavu 3 ľubovoľných lineárnych rovníc o 3 neznámych (x, y, z). Táto sústava lineárnych rovníc môže vyzerať napr. nasledovne:
R1 : x + 2y + z = 12
R2 : -y + 3z = 10
R3 : 3x + y - z = 3
Riešenie v SageMath
Príklad 2.
Nech je daná matica A = [[4,6,2],[6,9,1]] a matica B = [[8,5,2],[4,5,6]], ktoré sú rovnakého rozmeru.
Vypočítajte matice C, D, E, pričom C = A + B, D = A - B, E = B - A.
Riešenie v SageMath
Príklad 3.
Majme dané dve matice: A = [[1,2], [3,4], [5,6]] rozmeru 3x2, B = [[7,8,9], [10,11,12]] rozmeru 2x3.
Výpočítajte maticu C, ktorá je rovná súčinu AB a maticu D, ktorá je rovná súčinu BA.
Riešenie v SageMath
Príklad 4.
Vypočítajte hodnosť rozšírenej matice sústavy lineárnych rovníc:
2x1 + 8x3 = 2
4x1 + 2x2 + 4x3 = 0
6x1 +12x3 = 6
Riešenie v SageMath
Príklad 5.
Nájdite riešenie sústavy Ax = b uplatnením Frobeniovej vety.
Ax = b:
x1 + x2 + 3x3 = - 1
2x1 + x2 - 2x3 = 1
x1 + x2 + x3 = 3
x1 + 2x2 - 3x3 = 1
Riešenie v SageMath
Príklad 6.
Vypočítajte inverznú maticu k matici A = [[3,-2,4], [1,-12,16], [-6,0,-2]].
Následne overte, či platí vzťah A.A-1 = I vypočítaním tohto súčinu.
Riešenie v SageMath
Príklad 7.
Nájdite inverznú maticu k matici A = [[1,-1,2], [-2,3,3], [-1,3,0]] pomocou jednotkovej matice.
Využite pri tom algoritmus úpravy rozšírenej matice C = [A|I] na redukovaný Gaussov tvar, čím je možné získať maticu C´ = [I|A-1] v prípade, že je matica A invertovateľná.
Riešenie v SageMath
Príklad 8.
Majme danú sústavu rovníc Ax = b:
-4x1 + 2x2 + x3 - 5x4 = 6
3x2 - x3 + x4 = - 5
x1 + 6x2 +3x3 - x4 = 0
-x1 + 5x2 - x3 = - 4
Nájdite riešenie tejto sústavy.
Následne upravte túto sústavu rovníc do tvaru rozšírenej matice A,b a pomocou Gauss-Jordanovej eliminačnej metódy ju upravte na maticu C,d, ktorá je rozšírenou maticou sústavy Cx = d.
Nájdené riešenie by sa malo zhodovať s posledným stĺpcom (vektorom pravých strán) matice C,d.
Riešenie v SageMath
Príklad 9.
Vypočítajte determinant štvorcovej matice A = [[1,2,8], [3,2,3], [6,9,1]].
Riešenie v SageMath
Príklad 10.
Vypočítajte determinant ľubovoľnej matice rozmeru 3x3. Napr. matice M = [[2,15,-8], [3,0,5], [14,8,1]].
Riešenie v SageMath
Príklad 11.
Riešte sústavu rovníc Ax = b pomocou Cramerovho pravidla.
Ax = b :
6x1 - 4x2 + 8x3 = 6
4x1 - x2 + 2x3 = - 1
6x1 + 2x2 - 3x3 = - 15
Riešenie v SageMath
SageMath Cell


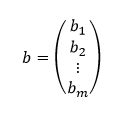
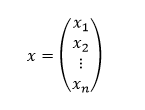
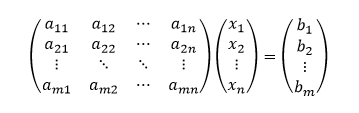

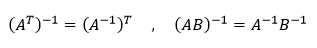
![C = [ A | I_n ]](../img/vzorec_vypocet_inverznej_matice_krok1.png)
![C´ = [ I_n | A^(-1) ]](../img/vzorec_vypocet_inverznej_matice_krok2.png)
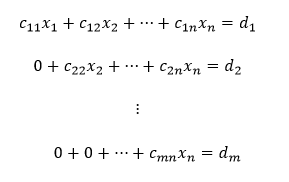
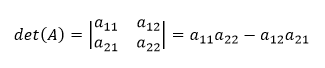
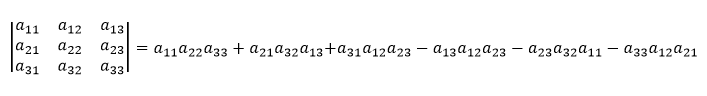
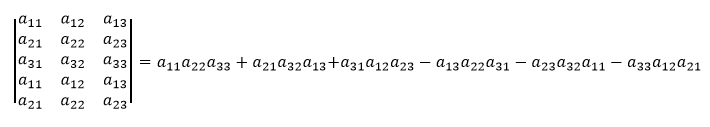
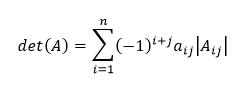
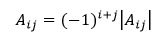
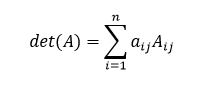
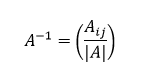
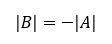
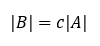
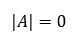
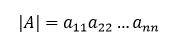
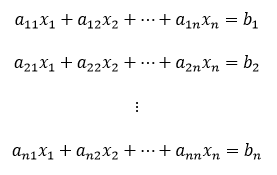

.png)