
Množiny
Prvým tematickým celkom, ktorý je súčasťou základného kurzu matematiky sú množiny čísel. Pre správne pochopenie nasledujúcich tém kurzu je dôležité, aby sme ovládali základné pojmy súvisiace s množinami. Dôležité je si predstaviť aj základné množiny čísel, vďaka čomu vieme určiť aj vlastnosti a správanie sa týchto čísel v rámci nasledujúcich častí.
Aj keď je možné predpokladať, že sme všetci so základnými číselnými množinami už dávno oboznámení, je dobré im pre zopakovanie venovať istú pozornosť.

Analytická geometria
Analytická geometria je oblasť matematiky, v ktorej sa študujú geometrické útvary pomocou ich analytických vyjadrení. Pomocou zvolenej súradnicovej sústavy je možné každý základný geometrický útvar vyjadriť jednoznačne v tvare istej rovnice (prípadne nerovnice).
Časť popisovaného kurzu nazývaná Analytické geometria jasne špecifikuje základné pojmy spojené s rovnomennou matematickou disciplínou. Týmito základmi teórie analytickej geometrie, ktoré sú v rámci tematického celku popísané sú: súradnicová sústava, vektory, rovnice rovinných útvarov, rovnice priestorových útvarov.

Lineárna algebra
Za sústavu lineárnych rovníc sa považuje množina viacerých lineárnych rovníc. Riešenie sústavy lineárnych rovníc sa uskutočňuje v rámci jednej zo základných matematických disciplín nazývanej lineárna algebra.
Jadrom časti s týmto názvom je práve problém riešenia sústavy lináernych rovníc. V tejto časti je priblížené, čo pod sústavou lineárnych rovníc rozumieme. Pomerne obsiahlym spôsobom sa venuje aj pojmom ako matice, Gaussove eliminačné metódy a determinanty.
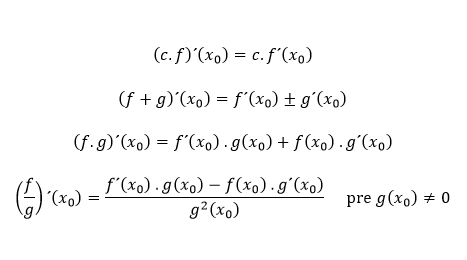
Diferenciálny počet
Veľkou súčasťou technických vied je skúmanie a popisovanie javov a ich vzájomných závislostí. Cieľom skúmania určitého javu môže byť zistenie okamžitého stavu javu alebo jeho celkového priebehu. Získavanie poznania o okamžitom stave javu na základe jeho priebehu je matematicky umožnené metódou rovnomennou s názvom tejto časti.
Základným pojmom diferenciálneho počtu, ale v podstate aj celej matematickej analýzy je tzv. derivácia, ktorá meria zmenu hodnôt závislej veličiny vzhľadom k zmene hodnôt nezávislej veličiny. K pochopeniu a správnemu použitiu derivácie je však potrebné najprv rozumieť pojmom ako funkcia, jej priebeh a limity funkcií, ktoré sú práve z tohto dôvodu zakomponované do tejto časti.

Integrálny počet
V rámci prírodných a technických vied je omnoho častejšie umožnené zistiť okamžitý stav javu, než jeho celkový priebeh. Práve tento problém matematicky rieši tzv. integrálny počet, ktorému je venovaná posledná časť popisovaného matematického kurzu. Je pravým opakom diferenciálneho počtu, spolu s ktorým je súčasťou infinitezimálneho počtu.
Tento tematický celok je pre lepšiu prehľadnosť rozdelený do viacerých častí. Vo všeobecnosti definuje integrál, no zároveň venuje osobitnú pozornosť určitému i neurčitému integrálu, ba dokonca aj nevlastným integrálom a ich aplikáciám.