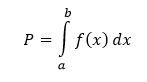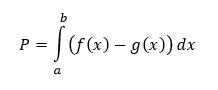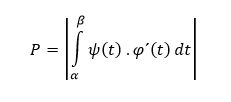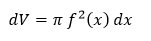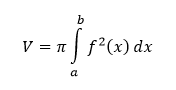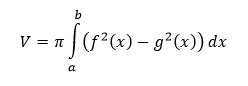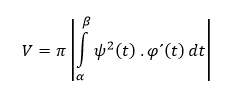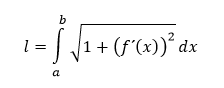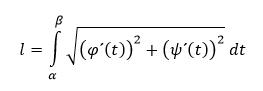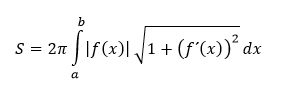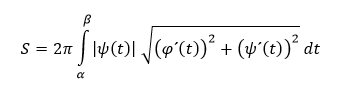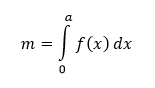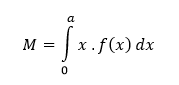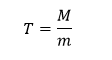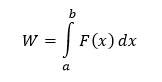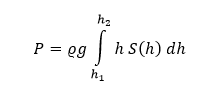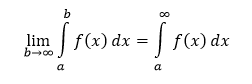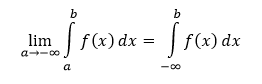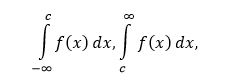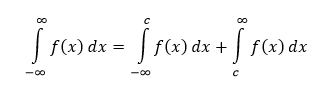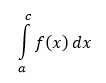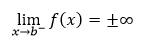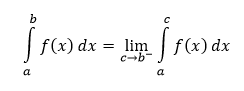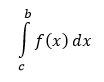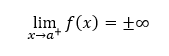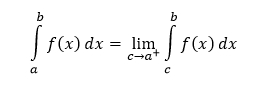Integrálny počet
Kľúčové slová:
integrál, infinitezimálny počet, neurčitý integrál, antiderivácia, primitívna funkcia, integračné pravidlá, metóda per partes, substitučná metóda, základné neuričté integrály, určitý integrál, oblasť pod krivkou, Riemannov súčet, Riemannov integrál, Newtonova - Leibnitzova formula, vlastnosti uričtých integrálov, homogenita integrandu, aditivita integrandu, aplikácie určitého určitého integrálu, obsah rovinnej oblasti, objemy rotačných telies, dĺžka krivky, obsah povrchu rotačnej plochy, fyzikálne aplikácie určitého integrálu, hmotnosť, statický moment, ťažisko, práca, tlak kvapaliny, nevlastné integrály, nevlastné integrály vplyvom hranice, nevlastné integrály vplyvom funkcie
V rámci prírodných a technických vied je omnoho častejšie umožnené zistiť okamžitý stav javu, než jeho celkový priebeh. Práve tento problém matematicky rieši tzv. integrálny počet.
Integrálny počet je matematická disciplína venujúca sa počítaniu integrálov. Spolu s diferenciálnym počtom je súčasťou oblasti matematiky nazývanej infinitezimálny počet. Základná veta tohto počtu hovorí, že derivácia a integrál sú v istom zmysle navzájom inverzné operácie. Integrálny počet sa totiž zaoberá otázkou toho, ako z okamžitého stavu javu odvodiť celkový obraz o jeho priebehu.
Pojem integrál
Pojem integrál je možné definovať z dvoch uhlov pohľadu.
O prvom uhle pohľadu už bolo pár slov povedaných. Integrál je možné chápať ako opak derivácie. V tomto zmysle slova ho môžeme teda nazvať aj antiderivácia. Zobrazenie integrálov ako opaku derivácie ukazuje, že integráciou a následnou diferenciáciou funkcie je možné sa v podstate dostať späť k tejto pôvodnej funkcii. Takýto uhol pohľadu vedie k definícii neurčitých integrálov.
Pri druhom uhle pohľadu rozumieme pod pojmom integrál oblasť pod krivkou. Tento uhol pohľadu naopak vedie k definícii určitých integrálov.
Neurčitý integrál
Definícia neurčitého integrálu vyplýva z uvažovania o integrácii ako o opaku derivácie. Inými slovami, cieľom takejto integrácie je nájsť k zadanej funkcii f(x) takú funkciu F(x), aby platilo
F´(x) = f(x)
Budeme sa teda snažiť zistiť, akú funkciu je potrebné derivovať, aby sme získali zadanú funkciu.
Nech funkcia f(x) je definovaná na intervale I. Funkcia F(x) sa nazýva primitívna, ak pre každé x ∈ I platí vyššie uvedený vzťah. Množina všetkých primitívnych funkcií k funkcii f(x) na intervale I sa nazýva neurčitý integrál z funkcie f(x), ktorý môžeme taktiež vyjadriť zápisom
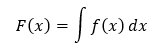
Dôležitou súčasťou tohto integrálu je dx – diferenciál premennej x, ktorý predstavuje nekonečne malú zmenu premennej a ukazuje, že premenná integrácie je x.
Neurčité integrály je možné definovať iba po konštantu, vzhľadom na to, že derivácia konštanty je 0. Toto tvrdenie v praxi znamená, že po nájdení primitívnej funkcie k danej funkcii, je možné k tejto primitívnej funkcii pridať ľubovoľnú konštantu a výsledná funkcia bude stále spĺňať stanovenú podmienku, ktorá vraví, že derivácia primitívnej funkcie sa má rovnať funkcii, ku ktorej primitívnu funkciu hľadáme.
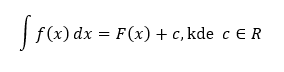
Základné integračné pravidlá a metódy
V zásade, ak integráciu vnímame ako opačnú operáciu k derivácii, tak v prípade, že vieme derivovať, mali by sme taktiež vedieť ako integrovať. Rovnako ako pre derivácie, aj pre integrály platia určité pravidlá a zásady, ktorými sa pri práci s nimi musíme riadiť.
Nech sú dané funkcie f a g, ktoré majú na intervale I primitívne funkcie, kde c ∈ R je ľubovoľná konštanta. Potom platia pravidlá:
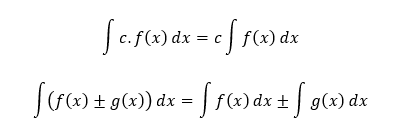
Okrem týchto pravidiel poznáme aj osobitné integračné metódy, ktorými sú metóda per partes a substitučná metóda.
Metóda per partes
Metóda per partes sa používa na integrovanie súčinu funkcií. Ide o metódu počítania neurčitých integrálov, ktorá je odvodená zo súčinu derivácií.
Nech funkcie u(x) a v(x) majú deriváciu na intervale I. Ak existuje aspoň jeden z nasledujúcich integrálov, potom v intervale I platí
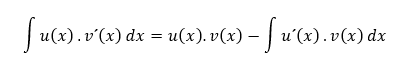
keďže platí vzťah
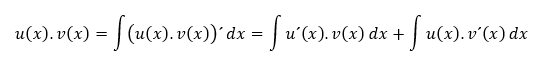
K tomu, aby sme dokázali napísať pravú stranu vzorca opisovanej metódy musíme vedieť derivovať aspoň jednu z funkcií integrálu na ľavej strane (v našom prípade u(x)) a druhú funkciu (v(x)) musíme vedieť integrovať. Zatiaľ, čo derivovať istú funkciu problémom byť nemusí, integrovať nejakú funkciu už problémom byť môže. V poslednom rade, by mal teda integrál na pravej strane byť jednoduchší z hľadiska ďalšej integrácie.
V niektorých prípadoch po použití tejto metódy nezískame jednoduchší integrál, ale iba jemu podobný. Po jej opakovanom použití však môžeme pôvodný integrál vyjadriť pomocou neho samého a z obdŕžanej rovnice ho vypočítať.
Substitučná metóda
Substitučná metóda je odvodená z derivácie zloženej funkcie. Principiálne spočíva na nasledujúcom tvrdení:
Nech funkcia F je na intervale I primitívna funkcia k funkcii f, a nech funkcia φ má v intervale J deriváciu, a pre každé x ∈ J je φ(x) ∈ I. Potom môžeme povedať, že
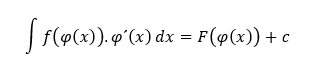
Praktický postup použitia substitučnej metódy pozostáva z týchto krokov:
- Hľadanie takej funkcie φ, ktorá sa v integrovanej funkcii nachádza spolu so svojou deriváciou alebo jej číselným násobkom
- Nahradenie (substitúcia) funkcie φ(x) za premennú t, tak, že platí t = φ(x)
- Úprava daného integrálu na tvar
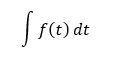
pričom dt = φ´(x)dx
- Počítanie nového výrazu
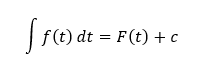
- Spätná substitúcia – nahradenie t spätne za φ(x) po nájdení takejto primitívnej funkcie
Základné neurčité integrály

Mnohé z užitočných neurčitých integrálov v skutočnosti nie je možné riešiť, z čoho vyplýva, že ich ani nemožno uviezť ako analytický výraz.
Určitý integrál
Základný rozdiel medzi určitým a neurčitým integrálom spočíva v tom, že zatiaľ, čo neurčitý integrál predstavuje množinu funkcií, určitý integrál je číslo. Pre definovanie určitého integrálu je nutné sa na integrál pozerať ako na oblasť pod krivkou, ktorá je grafom funkcie ohraničeného dolnou a hornou hranicou.
Riemannova definícia určitého integrálu
Majme danú funkciu f(x), ktorá je a intervale 〈a,b〉 spojitá a nezáporná, takže f(x) ≥ 0. Predstavme si, že chceme vypočítať obsah oblasti P pod jej grafom.
V prípade, že je funkcia lineárna alebo konštantná, je počítanie tejto oblasti jednoduché. Ide totiž o lichobežník, prípadne obdĺžnik. Vo všeobecnosti je však možné postupovať nasledovne:
- Danú oblasť, resp. interval 〈a,b〉 rozdelíme bodmi a = x1 < x2 < ⋯ < xn-1 < xn = b na n častí 〈xi-1, xi〉, ktoré nazývame podintervaly.
- V každom z týchto podintervalov zvolíme bod ti.
- V každom podintervale nahradíme príslušnú časť plochy obdĺžnikom, ktorého základňa má dĺžku (xi - xi-1) a výšku f(ti).
- Následne vypočítame súčet obsahov všetkých takýchto obdĺžnikov daný vzťahom
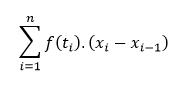

Presnosť tejto metódy výpočtu obsahu ohraničenej oblasti pod grafom závisí od veľkosti hodnoty n. Pokiaľ n = ∞, tak výsledok súčtu sa rovná obsahu oblasti pod grafom. Inými slovami, obsahom oblasti pod grafom, resp. určitým integrálom funkcie f(x) na intervale 〈a,b〉 je (v prípade, že existuje) limita
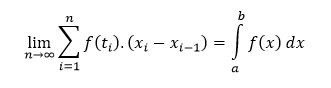
Newtonova - Leibnitzova formula
Nech je funkcia f(x) definovaná, ohraničená a integrovateľná na intervale 〈a,b〉 tak, že F(x) je primitívna funkcia, ktorá k nej existuje. Potom výraz
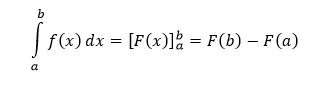
predstavuje určitý integrál z funkcie f(x) na intervale 〈a,b〉, inak povedané aj od a po b.
Vlastnosti určitých integrálov
Určitým integrálom môžeme prideliť nasledovné vlastnosti.

Nech sú dané funkcie f a g, ktoré sú integrovateľné na intervale 〈a,b〉. Potom sú na tomto intervale integrovateľné taktiež funkcie f(x) ± g(x) a c.f(x), kde c predstavuje konštantu a platí vlastnosť
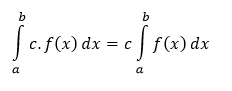
ktorú nazývame homogenita integrandu a vlastnosť
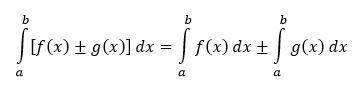
ktorú nazývame aditivita integrandu.
Rovnako ako pre počítanie neurčitých integrálov, aj pre počítanie určitých integrálov môžeme využiť metódu per partes, podľa ktorej platí
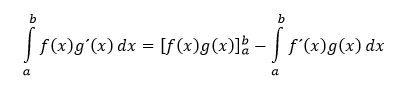
a substitučnú metódu, na základe ktorej pre určité integrály zložených funkcií platí
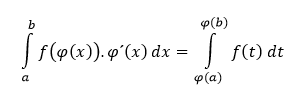
kde t = φ(x).
Ďalšia vlastnosť určitého integrálu vraví, že v prípade, že funkcie f(x) ≤ g(x) sú na intervale 〈a,b〉 integrovateľné, tak pre určité integrály týchto funkcií v danom intervale platí vzťah
≤g(x).png)
Aplikácie určitého integrálu
Určité integrály je možné v praxi použiť k výpočtu mnohých vecí a v rozličných vedných disciplínach, akými sú napr. geometria a fyzika.
Obsah rovinnej oblasti
Obsah rovinnej oblasti ohraničenej v intervale 〈a,b〉 grafom funkcie f, priamkami x = a, x = b a osou x počítame pomocou určitého integrálu
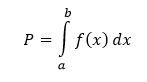
Obsah rovinnej oblasti, ktorá je na intervale 〈a,b〉 ohraničená grafmi funkcií f ≥ g, a priamkami x = a, x = b počítame ako určitý integrál
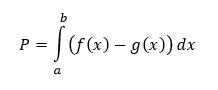
V prípade, že je parametrická krivka daná dvojicou funkcií x = φ(t), y = ψ(t), pričom t ∈ 〈α,β〉. K odvodeniu vzorca pre výpočet obsahu oblasti, ktorej hranice sú dané parametricky, spravíme v prvom z uvedených vzorcov substitúciu x = φ(t) a dx = φ´(t) dt, pričom vieme, že y = ψ(t) = f(φ(t)). Následne dostávame vzťah
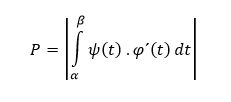
Objem rotačných telies
Majme danú plochu P, ktorá vytvára rotačné teleso tým, že rotuje okolo osi x. Pomyselným rozrezaním vzniknutého telesa na plátky hrúbky dx, ktorých obsah je π f2(x) tak, aby sme mohli zanedbať zaoblenie jeho povrchu, dostaneme jeden element objemu tohto telesa, ktorého veľkosť je daná vzťahom
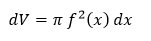
Potom celkový objem tohto rotačného telesa vzniknutého rotáciou rovinnej oblasti ohraničenej v intervale 〈a, b〉 grafom funkcie f ≥ 0, priamkami x = a, x = b a osou x, okolo osi x počítame pomocou určitého integrálu
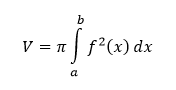
Objem rotačného telesa vzniknutého rotáciou rovinnej oblasti, ktorá je v intervale 〈a,b〉 ohraničená grafmi funkcií f ≥ g ≥ 0, priamkami x = a, x = b okolo osi x počítame ako určitý integrál
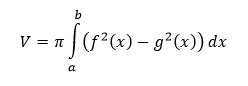
V prípade, že sú oblasti určené uzavretou krivkou dané parametricky, objem rotačného telesa počítame ako určitý integrál
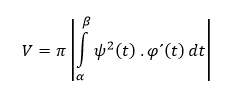
Dĺžka krivky
Dĺžku rovinnej krivky, ktorá je grafom funkcie f, o ktorej môžeme povedať že má na intervale 〈a,b〉 spojitú deriváciu, vypočítame vzťahom
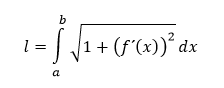
ktorého základ je postavený na použití Pytagorovej vety.
V prípade, že je spomínaná krivka určená parametrickými rovnicami x = φ(t), y = ψ(t), kde t ∈ 〈α,β〉 a derivácie φ´(t), ψ´(t) sú v intervale 〈α,β〉 spojité, tak dĺžku tejto rovinnej krivky počítame ako
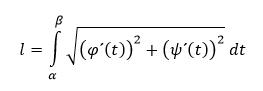
Obsah povrchu rotačnej plochy
Obsah povrchu rotačnej plochy vzniknutej rotáciou grafu funkcie f v intervale 〈a,b〉 okolo osi x počítame prostredníctvom vzťahu
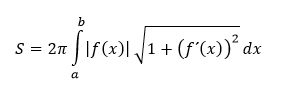
Ak rotačná plocha vznikne rotáciou uzavretej krivky určenej viackrát spomínanými parametrickými rovnicami okolo osi x, tak obsah tejto rotačnej plochy vypočítame ako určitý integrál
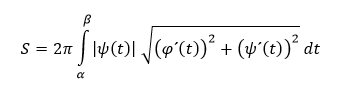
Fyzikálne aplikácie určitého integrálu
Hmotnosť, statický moment a ťažisko
Nech funkcia f definovaná na intervale 〈0,a〉 reprezentuje jednorozmernú hustotu tyče dĺžky a. Potom
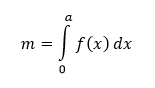
predstavuje jej hmotnosť,
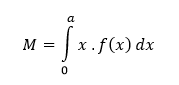
predstavuje statický moment a
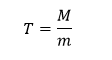
predstavuje ťažisko definovanej tyče.
Práca
Mechanickú prácu vykonanú silou F(x) pôsobiacou na intervale 〈a,b〉 môžeme počítať ako
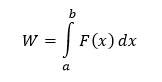
Tlak kvapaliny
Určitý integrál je taktiež možné použiť k výpočtu celkového tlaku kvapaliny pri meniacej sa hĺbke, a to konkrétne vzťahom
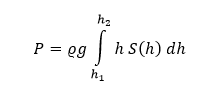
kde h1, h2 sú hranice sú hranice hĺbky, ϱ predstavuje hustotu kvapaliny, g je gravitačná konštanta a S(h) je veľkosť plochy, na ktorú v hĺbke h tlak pôsobí.
Nevlastné integrály
Pod pojmom nevlastný integrál rozumieme taký určitý integrál, ktorého interval alebo funkcia sú neohraničené. Na základe toho, o ktorý prípad ide rozdeľujeme tieto integrály na:
- nevlastné integrály vplyvom hranice, ak je intervalom integrácie ⟨a,∞), (-∞,b⟩ alebo (-∞,∞)
- nevlastné integrály vplyvom funkcie, ak je funkcia integrovaná na intervale 〈a,b〉 neohraničená (nespojitá) v bode a, b, c ∈ (a,b) alebo v bodoch a aj b
- nevlastné integrály, ktoré sú kombináciou menovaných druhov
Nevlastné integrály vplyvom hranice
Nech je funkcia f(x) definovaná na intervale ⟨a,∞) a integrovateľná na intervale 〈a,b〉 pre každé b > a. Potom nevlastným integrálom funkcie f(x) nazývame vlastnú limitu
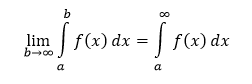
Ak je funkcia f(x) na intervale ⟨a,∞) spojitá a nezáporná, potom pre ľubovoľné b > a tento nevlastný integrál určuje obsah krivočiareho lichobežníka. Ak takýto nevlastný integrál pre b → ∞ konverguje, tak jeho hodnotu považujeme za obsah nekonečnej rovinnej oblasti zhora ohraničenej grafom funkcie, zdola ohraničenej osou x a zľava priamkou x = a.
Nech je funkcia f(x) tentokrát definovaná na intervale (-∞,b⟩ pre každé a < b. V tom prípade je nevlastným integrálom funkcie f(x) vlastná limita
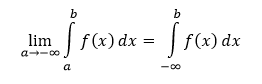
Ak je funkcia f(x) na intervale (-∞,b⟩ spojitá a nezáporná, potom pre ľubovoľné a < b tento nevlastný integrál určuje obsah krivočiareho lichobežníka. Ak takýto nevlastný integrál pre a → -∞ konverguje, tak jeho hodnotu považujeme za obsah nekonečnej rovinnej oblasti ohraničenej zhora grafom funkcie, zdola osou x a sprava priamkou x = b.
O týchto nevlastných integráloch môžeme povedať, že
- konvergujú, ak dané vlastné limity existujú
- divergujú, ak dané limity neexistujú alebo sú nevlastné
V poslednom rade môžeme hovoriť o nevlastnom integráli na obojstranne neohraničenom intervale. Nech je funkcia f(x) definovaná na intervale (-∞,∞) a c ∈ R. Ak existujú nevlastné integrály
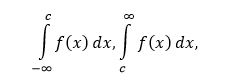
potom je nevlastným integrálom funkcie f(x) na intervale (-∞,∞) ich súčet.
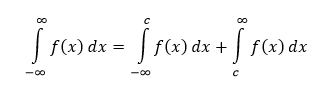
Tento nevlastný integrál diverguje, ak diverguje čo i len jeden z nevlastných integrálov súčtu. Ak je funkcia f(x) na intervale (-∞,∞) spojitá a nezáporná a nevlastný integrál tejto funkcie konverguje, tak jeho hodnotu považujeme za obsah nekonečnej rovinnej oblasti zhora ohraničenej grafom funkcie a zdola ohraničenej osou x.
Nevlastné integrály vplyvom funkcie
Majme daný interval 〈a,b〉 a takú funkciu f, že pre každé c ∈ ⟨a,b) existuje určitý integrál
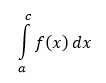
a limita
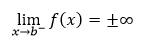
Potom je bod b singulárnym, alebo inak povedané aj kritickým bodom a nevlastný integrál tejto funkcie vypočítame ako
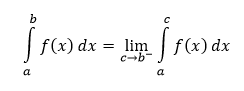
V prípade, že pre každé c ∈ (a,b⟩ existuje určitý integrál
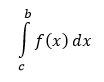
a limita
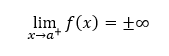
Potom je singulárnym, resp. kritickým bodom funkcie bod a a jej nevlastným integrálom je
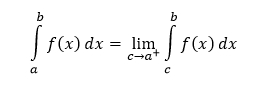
O týchto nevlastných integráloch môžeme takisto povedať, že vyjadrujú obsah nekonečných rovinných oblastí a že
- konvergujú, ak sú tieto limity vlastné
- divergujú, ak dané limity neexistujú alebo sú nevlastné
Úlohy
Príklad 1.
Vypočítajte primitívnu funkciu (antideriváciu) ľubovoľnej funkcie f(x). Napr.: 6.cos(x) + 3.
Riešenie v SageMath
Príklad 2.
Utvorte neurčitý integrál ľubovoľnej funkcie f(x), napr.: 4x2. Funkciu f(x) a jej primitívnu funkciu F(x) následne graficky znázornite.
Riešenie v SageMath
Príklad 3.
Rozdeľte oblasť pod grafom ľubovoľnej funkcie na intervale 〈a,b〉 na n častí - obdĺžnikov.
Napr. oblasť pod grafom funkcie sin(x) v intervale 〈0,1.5π〉 na 19 častí.
Riešenie v SageMath
Modifikácia úlohy z knihy:
RAZVAN, A. MEZEI.: An Introduction to Sage Programming – With Applications to SAGE Interacts for Numerical Methods. New Jersey, USA. John Wiley & Sons, Inc., 2016. 245 s. ISBN 9781119122784
Príklad 4.
Zistite Riemannov súčet ľubovoľnej funkcie na intervale 〈a,b〉 a výpočítajte jej určitý integrál ako limitu Riemannovho súčtu pre n → ∞.
Napr. pre funkciu 3x2 na intervale 〈3,6〉.
Riešenie v SageMath
Modifikácia úlohy z knihy:
RAZVAN, A. MEZEI.: An Introduction to Sage Programming – With Applications to SAGE Interacts for Numerical Methods. New Jersey, USA. John Wiley & Sons, Inc., 2016. 245 s. ISBN 9781119122784
Príklad 5.
Vypočítajte určitý integrál funkcie f(x): 3x2 na intervale 〈10,24〉 pomocou Newtonovej - Leibnitzovej formuly.
Riešenie v SageMath
Príklad 6.
Vypočítajte určitý integrál ľubovoľnej funkcie na intervale 〈a,b〉 pomocou Newtonovej - Leibnitzovej formuly.
Riešenie v SageMath
Príklad 7.
Vypočítajte určitý integrál funkcie 2.sin(x) na intervale 〈0,π〉.
Riešenie v SageMath
Príklad 8.
Vypočítajte určitý integrál ľubovoľnej funkcie, napr.: 6.x2+x na intervale 〈a,b〉, napr.: 〈-2,12〉.
Riešenie v SageMath
Príklad 9.
Vypočítajte určitý integrál ľubovoľnej funkcie, napr.: sin(x) na intervale 〈a,b〉, napr.: 〈0,1.5π〉 a zároveň zobrazte oblasť, ktorej obsah tento určitý integrál vyjaduje.
Riešenie v SageMath
Príklad 10.
Vypočítajte pomocou určitého integrálu dĺžku krivky grafu funkcie sin(x) na intervale 〈0,1.5π〉.
Riešenie v SageMath
Príklad 11.
Vypočítajte objem rotačného telesa vytvoreného rotáciou rovinnej oblasti určenej grafom funkcie sin(x) na intervale 〈-1,2〉. Toto teleso následne zobrazte.
Riešenie v SageMath
Príklad 12.
Zobrazte rotačné teleso vzniknuté rotáciou 2 ľubovoľných funkcií okolo osi x na intervale 〈a,b〉. Vypočítajte taktiež jeho objem.
Prvotným rotačným telesom nech je teleso dané funkciami f(x): x2 a g(x): x na intervale 〈0,1〉.
Riešenie v SageMath
SageMath Cell
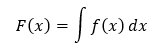
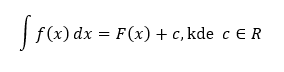
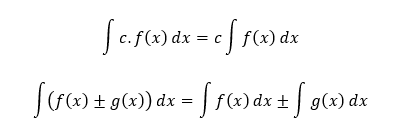
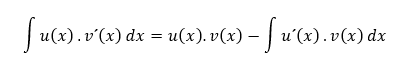
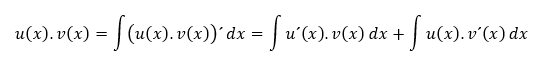
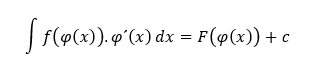
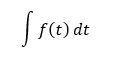
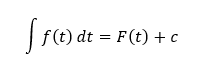

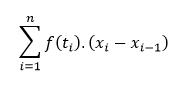

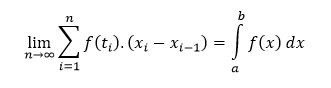
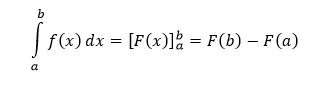

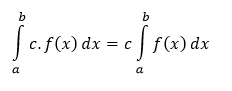
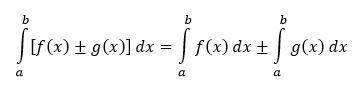
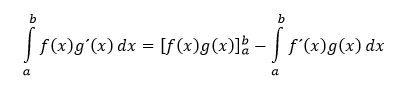
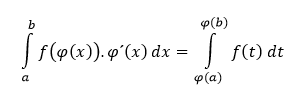
≤g(x).png)