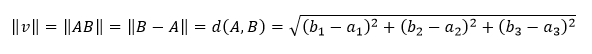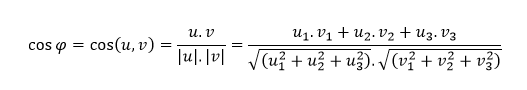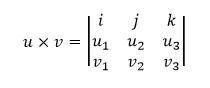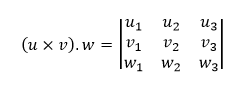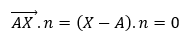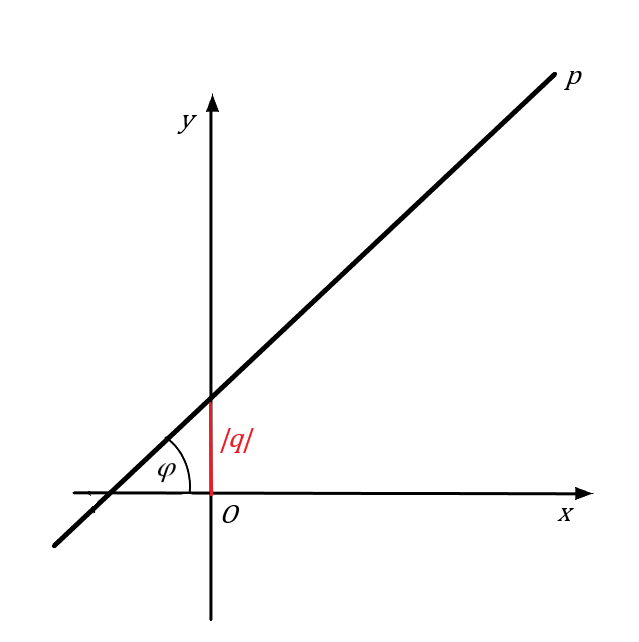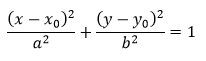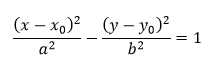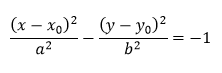Analytická geometria

Kľúčové slová:
analytická geometria, súradnicové sústavy, súradnice, rovina, priestor, vektor, súradnice vektora, dĺžka vektora, polohový vektor, nulový vektor, jednotkový vektor, kolineárnosť a komplanárnosť vektorov, skalárny súčin vektora a konštanty, súčet vektorov, rozdiel vektorov, lineárna kombinácia vektorov, skalárny súčin vektorov, uhol vektorov, vektorový súčin, zmiešaný súčin vektorov, rovnice rovinných útvarov, normálová rovnica priamky, všeobecná rovnica priamky a polroviny, smernicová rovnica priamky, smernica, parametrická rovnica priamky, parametrická rovnica polpriamky, parametrická rovnica úsečky, rovnice kužeľosečiek, rovnica kružnice, rovnica elypsy, rovnica praboly, rovnica hyperboly, rovnice priestorových útvarov, normálová rovnica roviny, všeobecná rovnica roviny a polpriestora, parametrická rovnica priamky v priestore, parametrická rovnica roviny, rovnica guľovej plochy

Analytická geometria, nazývaná aj súradnicová geometria, je oblasť matematiky, v ktorej sa geometrické útvary študujú pomocou ich analytických vyjadrení. So zvolenou súradnicovou sústavou vieme každý zo základných geometrických útvarov jednoznačne vyjadriť v tvare rovnice alebo nerovnice. Pričom vzťah medzi určitým geometrickým útvarom a jemu prislúchajúcou rovnicou (nerovnicou) je daný nasledovným pravidlom:

Na základe tohto pravidla je prienikom útvarov U₁ a U₂ množina všetkých bodov, ktoré súčasne spĺňajú rovnice (nerovnice) oboch týchto útvarov.

Dôležitosť analytickej geometrie spočíva práve v tom, že vytvára spojenie medzi geometriou a algebrickými výrazmi, čím umožňuje preformulovať problémy v geometrii ako problémy v algebre a naopak. Vďaka tomu môžu byť metódy jednej matematickej disciplíny použité na riešenie problémov tej druhej.

Súradnicové sústavy

Pre potreby analytickej geometrie sa využívajú najmä karteziánske súradnicové sústavy. Karteziánska súradnicová sústava je sústavou navzájom na seba kolmých priamok, ktoré voláme osi súradnicovej sústavy. Tieto osi majú jediný spoločný bod, ktorý sa nazýva začiatok súradnicovej sústavy a označuje sa znakom O. Každá os je bodmi, ktoré na nej ležia rozdelená na rovnako veľké diely počnúc bodom O. Vzdialenosť medzi týmito bodmi, resp. veľkosť týchto dielov určuje jednotku dĺžky danej osi.

Karteziánska súradnicová sústava je prostriedok, pomocou ktorého vieme každému bodu jednoznačne priradiť usporiadanú n-ticu reálnych čísel, ktoré voláme súradnice daného bodu. Na základe toho, koľko súradníc daný bod má, vieme určiť či sa nachádza v rovine alebo v priestore.

Rovina
Karteziánska sústava v rovine je súradnicová sústava, ktorá ma dve osi (x,y), z čoho vyplýva, že aj bod v nej ležiaci má práve 2 zložky (súradnice):

• x-ová súradnica – určuje vzdialenosť a polohu bodu voči osi y, pri umiestnení bodu vpravo od y-ovej osi nadobúda + hodnoty, pri umiestnení vľavo - hodnoty;
• y-ová súradnica – určuje vzdialenosť a polohu bodu voči osi x, pri umiestnení bodu nahor od x-ovej osi nadobúda + hodnoty, pri umiestnení bodu nadol - hodnoty.

Takto určená súradnicová sústava rozdeľuje rovinu na 4 časti (kvadranty): [+,+], [-, +], [-,-], [+, -].

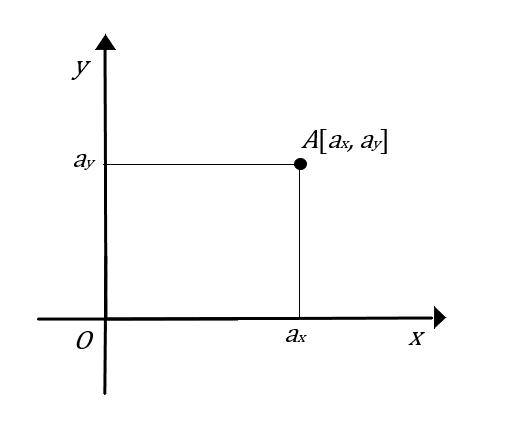
Fakt, že bod A má súradnice a_x, a_y značíme zápisom A[a_x, a_y] alebo A = [ a_x, a_y ].

Priestor
Karteziánska sústava v priestore je sústavou zvyčajne tvorenou 3 osami (x,y,z), ktoré vytvárajú 3 súradnicové roviny. Pre ľahšie pochopenie takejto súradnicovej sústavy môžeme použiť nasledovnú analógiu.

Nech bod O je bodom, kde sa steny v rohu miestnosti stretávajú s podlahou, potom platí:

1. Os x je vodorovná čiara, pozdĺž ktorej sa stena po našej ľavici pretína s podlahou.
2. Os y je vodorovná čiara, pozdĺž ktorej sa stena po našej pravici pretína s podlahou.
3. Os z je zvislá čiara, v ktorej sa pretínajú steny.
4. Kladnými časťami osí sú čiary, ktoré vidíme, keď stojíme v miestnosti.
5. Zápornými časťami osí sú pokračovania týchto čiar mimo miestnosti.

Bod ležiaci v priestore má práve 3 súradnice: x-ovú, y-ovú a z-ovú, ktoré určujú jeho vzdialenosť od súradnicových rovín: yz, xz a xy presne v takomto poradí.

Skutočnosť, že bod A sa nachádza v 3-rozmernom priestore a má súradnice a_x, a_y, a_z zapisujeme spôsobom A[ a_x, a_y, a_z ] alebo A = [ a_x, a_y, a_z ].

Vektory

Karteziánske súradnice je možné použiť nielen na určenie polohy bodov, ale aj na určenie súradníc vektorov. Pre prácu s vektormi je nutné rozumieť istým základným pojmom.

Vektor
Vektor je geometrický objekt určený dĺžkou, smerom a orientáciou. Je možné si ho predstaviť ako orientovanú úsečku – úsečku, na ktorej je vyznačený začiatočný a koncový bod. Býva znázornený ako šípka, čo sa prenieslo aj do spôsobu jeho notácie. Často ho totiž zapisujeme ako písmeno, nad ktorým je malá šípka. Ujalo sa však aj jeho značenie hrubou tlačou. Platí, že dve rôzne orientované úsečky s rovnakou dĺžkou (veľkosťou), smerom a orientáciou, predstavujú ten istý vektor s dvoma odlišnými umiestneniami.

Súradnice vektora
Súradnice vektora sú rozdielom súradníc bodov, ktorými je určený. Fakt, že vektor v má v trojrozmernom priestore súradnice v₁, v₂, v₃ uvádzame zápisom v [ v₁, v₂, v₃ ]. Ak je bod A [ a₁, a₂, a₃ ] začiatočným bodom vektora v a bod B [b₁, b₂, b₃] je jeho koncovým bodom, potom vektor v má súradnice [ b₁ - a₁, b₂ - a₂, b₃ - a₃ ]. Označujeme ho tiež ako B - A.

Dĺžka vektora
Dĺžka vektora je vzdialenosťou jeho začiatočného a koncového bodu. Dĺžka vektora v je označovaná ako ‖v‖ a vďaka uplatneniu Pytagorovej vety platí

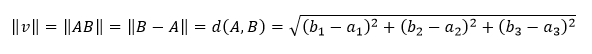
Polohový vektor
Pod pojmom polohový vektor rozumieme vektor začínajúci v začiatku súradnicovej sústavy končiaci v určitom bode. Polohovým vektorom bodu A je vektor A - O.

Nulový vektor
Nulový vektor je výsledkom odčítania vektora od seba samého. Je to jediný vektor, ktorého dĺžka je nulová. Všetky súradnice tohto vektora sú rovné 0. Označujeme ho znakom 0.

Jednotkový vektor
Jednotkový vektor je vektor vznikajúci vydelením vektora svojou vlastnou dĺžkou. Jeho dĺžka je tak rovná 1. Jednotkový vektor orientovaný v kladnom smere osi x označujeme písmenom i, jednotkový vektor orientovaný v kladnom smere osi y označujeme písmenom j a jednotkový vektor orientovaný v kladnom smere osi z označujeme ako k. Práve tieto vektory i, j, k tvoria bázu trojrozmerného priestoru.

Kolineárnosť a komplanárnosť vektorov
Kolineárne vektory sú vektory, ktorých obrazy ležia na navzájom rovnobežných, prípadne splývajúcich priamkach. Nekolineárne sú ich opakom.

Komplanárnými vektormi sú vektory ležiace v tej istej rovine alebo v rovinách, ktoré sú navzájom rovnobežné. V opačnom prípade ich nazývame nekomplanárne.

Skalárny súčin vektora a konštanty

Pre vektor v a skalárny násobok vektora v číslom c ∈ R, ktorý zapisujeme ako vektor c.v (v súradniciach c.v = [ cv₁, cv₂, cv₃ ] ) platí:

• dĺžka vektora c.v je |c| násobkom dĺžky vektora v;
• ak c > 0, tak vektory v a c.v sú rovnako orientované;
• ak c < 0, tak vektory v a c.v sú opačne orientované;
• ak c = 0, tak aj vektor c.v = 0;
• ak c = -1, tak c.v je opačným vektorom k vektoru v a značíme ho ako –v, pričom -v [ -v₁, -v₂, -v₃ ];
• ak je jeden z nich skalárnym násobkom toho druhého, tak sú rovnobežné a podiely ich prvých druhých a tretích súradníc sú zhodné.

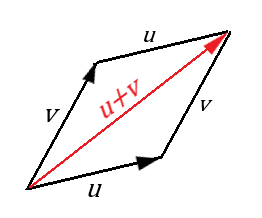
Súčet vektorov

Nech vektor v = AB a u = AC, potom ich súčet je vektor u + v = AB + AC. Súčet týchto vektorov môžeme pomocou súradníc zapísať v tvare

Vektor u+v môžeme znázorniť ako uhlopriečku rovnobežníka, ktorého stenami sú vektory u a v. Ich orientácia je znázornená na obrázku

Rozdiel vektorov

Rozdiel vektorov u a v je vektor

Geometricky je odčítanie vektorov u - v možné znázorniť tak, že sa vezme uhlopriečka rovnobežníka preklenutého vektorom u a vektor -v, ktorý je opačným vektorom vektora v.

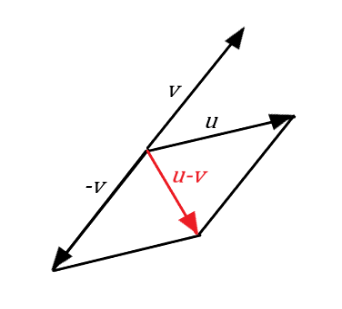
Lineárna kombinácia vektorov

Lineárna kombinácia vektorov u a v je výraz v tvare

Lineárnou kombináciou vektorov u, v a w je výraz

Čísla c, d a e sú v tomto prípade koeficientami kombinácie. Pre každú konkrétnu hodnotu koeficientov získavame konkrétny vektor.

Ak sú v rovine dané dva nerovnobežné vektory (nekolineárne), tak každý vektor tejto roviny sa dá vyjadriť ako lineárna kombinácia daných vektorov. Ak máme v priestore dané tri nekomplanárne vektory, tak každý vektor tohto priestoru sa dá vyjadriť lineárnou kombináciou týchto vektorov.

Vzhľadom na platnosť týchto tvrdení vieme každý vektor napísať v tvare lineárnej kombinácie vektorov bázy, kde koeficientami kombinácie sú súradnice vektora. Pre vektor u tak získavame výraz v tvare

Skalárny súčin vektorov

Skalárny súčin vektorov je jedinou operáciou s vektormi, ktorej výsledkom nie je vektor, ale skalár (konštanta). Skalárny súčin vektorov u a v je číslo

Tento vzťah môžeme pomocou súradníc zapísať ako

Skalárny súčin vektorov sa rovná 0, ak sa aspoň jeden z nich rovná 0 alebo aj vtedy, ak sú nenulové, ale uhol medzi nimi je rovný 90°.

Uhol vektorov

Uhol φ, ktorý je uhlom vektorov u = [ u₁, u₂, u₃ ] a v = [ v₁, v₂, v₃ ] dokážeme vypočítať pomocou vzťahu

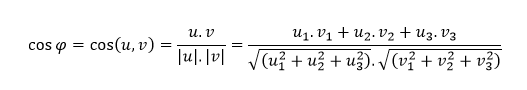
Z definície skalárneho súčinu vektorov a vlastností funkcie cos vyplýva:

• ak u.v > 0, tak uhol týchto vektorov je ostrý;
• ak u.v < 0, tak uhol týchto vektorov je tupý;
• ak u.v = 0, tak uhol týchto vektorov je pravý.

Vektorový súčin

Vektorový súčin dvoch vektorov u a v, ktorý značíme ako u × v, je súčinom absolútnych hodnôt týchto vektorov a sin uhla nimi zovretého, ktorý je kolmý na smer oboch vektorov a orientovaný tak, aby bol systém tvorený trojicou usporiadaných vektorov [ u, v, u × v ] pravotočivou sústavou. Túto definíciu algebricky vyjadrujeme zápisom

V súradniciach môžeme vektorový súčin u × v vyjadriť ako determinant matice:

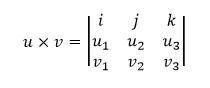
Termín determinant je bližšie vysvetlený v časti Lineárna algebra.

Geometrický význam tejto operácie s vektormi spočíva v tom, že dĺžka vektorového súčinu dvoch vektorov je rovná veľkosti plošného obsahu rovnobežníka vytvoreného týmito vektormi.

Zmiešaný súčin vektorov

Okrem samostatného skalárneho a vektorového súčinu vektorov poznáme aj zmiešaný súčin vektorov. Zmiešaný súčin vektorov u, v a w je súčin (u × v).w, ktorý je pomocou súradníc možné rozpísať ako výraz

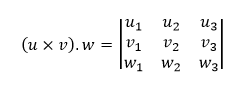
Vyplývajúc z definície, podľa ktorej sa skalárny súčin vykonáva ako posledný, je zmiešaný súčin číslo závisiace od troch vektorov.

Geometrický význam zmiešaného súčinu vektorov spočíva v tom, že jeho absolútna hodnota je rovná objemu rovnobežnostena vytvoreného týmito troma vektormi umiestnenými v spoločnom začiatku.

Rovnice rovinných útvarov

Rovnica rovinného útvaru je vo všeobecnosti rovnicou s dvomi neznámymi x a y, ktorá určuje tento útvar na základe vyššie spomínaného pravidla. Spôsob, akým získame rovnicu útvaru, závisí od toho aké informácie o útvare sú k dispozícii. V rôznych situáciách je možné dostať rôzne typy rovníc.

Normálová rovnica priamky

Normálový vektor priamky p je každý vektor kolmý na túto priamku.

Predpokladajme, že poznáme súradnice bodu A[ x₀, y₀ ], ktorým je priamka určená a niektorý jej normálový vektor n. Potom ľubovoľný bod roviny X[ x, y ] leží na danej priamke práve vtedy, ak vektory X - A a n sú navzájom kolmé. Na základe týchto vlastností skalárneho súčinu získavame normálovú rovnicu priamky:

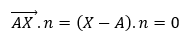
Rozpísaním tejto rovnice v súradniciach, dostaneme všeobecnú rovnicu danej priamky.

Všeobecná rovnica priamkya polroviny

Všeobecná rovnica priamky je rovnica v tvare:

Geometrický význam týchto čísel spočíva v tom, že existuje normálový vektor n = [ a, b ] a číslo c, ktoré je rovné skalárnemu súčinu polohového vektora ľubovoľného bodu priamky s týmto normálovým vektorom. Ak X je ľubovoľný bod priamky, tak

Absolútna hodnota tohto čísla |c| je priamo úmerná vzdialenosti priamky od začiatku súradnicovej sústavy O.

Polroviny určené touto priamkou zapisujeme ako nerovnice

Každá priamka má v rovine nekonečne veľa všeobecných rovníc, ktoré sú nenulovým násobkom jednej z nich.

Smernicová rovnica priamky

Smernicová rovnica je rovnica napísaná v tvare:

Takzvanou smernicou priamky je číslo k, ktoré je rovné tangensu uhla priamky s kladnou polosou osi x. Z toho vyplýva, že smernicu priamky môžeme zapísať ako

Pre priamky rovnobežné s osou y neexistuje smernicová rovnica, keďže s osou x zvierajú uhol 90°, ktorého tangens nie je definovaný. Ak k = 0 jedná sa o priamku rovnobežnú s osou x.

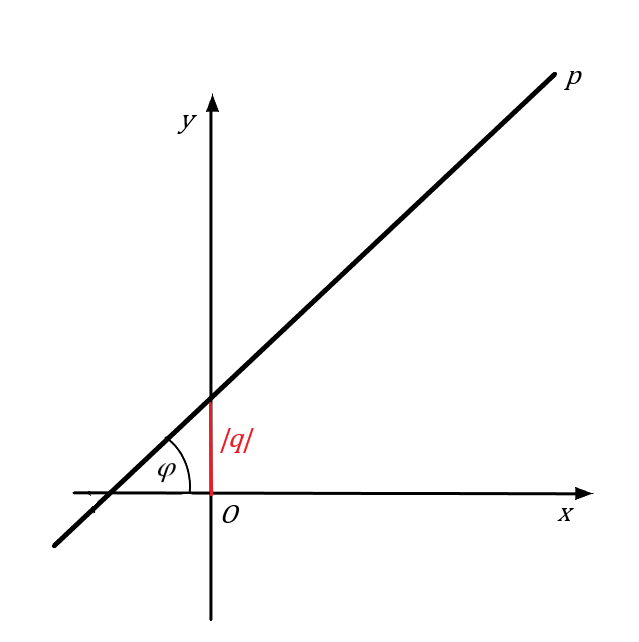
Číslo q nazývané aj úsek priamky je y-ovou súradnicou priesečníka priamky s osou y. Smernica priamky tak vyjadruje zmenu závislej premennej y pri zmene nezávislej premennej x.

Rovnicou priamky prechádzajúcej bodom [ x₀, y₀ ] so smernicou k je

z čoho vyplýva, že platí

Aby sme mohli zistiť smernicovú rovnicu priamky väčšinou musíme poznať jej smerový vektor a niektorý bod. Smerový vektor priamky p je každý vektor rovnobežný s touto priamkou. Vzhľadom na to môžeme pomocou vyššie uvedeného vzorca získať smernicu rovnice, keďže tangens uhla môžeme vypočítať ako podiel protiľahlej a priľahlej odvesny. Číslo q získame dosadením súradníc daného bodu do smernicovej rovnice.

Parametrické rovnice priamky, polpriamky a úsečky

Ak máme daný niektorý bod priamky X₀ = [ x₀, y₀ ] a jej smerový vektor s [ s₁, s₂ ], tak ľubovoľný bod roviny X = [ x, y ] leží na danej priamke práve vtedy, ak sú vektory X - X₀ a s navzájom rovnobežné. Potom existuje číslo t ∈ R (parameter), pre ktoré platí

Ak túto rovnicu rozpíšeme pomocou daných súradníc získame parametrické rovnice priamky:

Parametrické rovnice priamky je taktiež možné napísať vo vektorovom tvare

Parametrické rovnice polpriamky určenej bodom X₀ = [ x₀, y₀ ] a smerovým vektorom s [s₁, s₂ ] majú tvar

Úsečka AB stanovená bodmi A [a₁, a₂ ] a B [b₁, b₂ ] má parametrické rovnice

Rovnice kužeľosečiek

Kužeľosečka je rovinná krivka vzniknutá rezom rotačnej kužeľovej plochy rovinou neprechádzajúcou jej vrcholom. Vzhľadom na sklon roviny rezu voči osi kužeľovej plochy vznikajú druhy útvarov ako kružnica, elipsa, parabola a hyperbola.

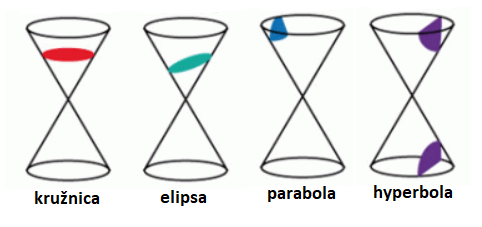
Kružnica
Krivka vznikajúca rezom dvoj-kužeľa rovinou kolmou na jej os je kružnica. Kružnica je množina bodov s rovnakou vzdialenosťou r (polomer kružnice) od bodu S = [ x₀, y₀ ], ktorý je jej stredom. Rovnica kružnice má tvar:

Jej prevedením na všeobecnú rovnicu získame rovnicu

Elipsa
Geometrický útvar nazývaný elipsa vzniká rezom dvoj-kužeľa šikmou rovinou. Elipsu je možné definovať ako množinu všetkých bodov roviny, ktorých súčet vzdialeností od dvoch rôznych bodov je konštantný a väčší ako vzdialenosť daných bodov, nazývaných ohniská. Elipsa so stredom S = [ x₀, y₀ ] a polosami dĺžok a, b je vyjadrená rovnicou

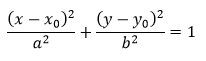
Parabola
Parabola je krivkou vznikajúcou „otvoreným“ rezom dvoj-kužeľa šikmou rovinou. Odbornejšie povedané je parabola množinou bodov s rovnakou vzdialenosťou od priamky a od bodu, ktorý na nej neleží, t.j. množina bodov, ktorých podiel vzdialeností od daného bodu a priamky je rovný 1. Parabola s vrcholom V = [ x₀, y₀ ] a parametrom p má rovnicu v tvare

Hyperbola
Dvojitým rezom dvoj-kužeľa rovinou rovnobežnou s jeho osou vzniká hyperbola. Je to množina všetkých bodov roviny, ktorých rozdiel vzdialeností v absolútnej hodnote od daných dvoch rôznych bodov je konštantný a menší ako ich vzájomná vzdialenosť. Dané body sa nazývajú ohniská hyperboly. Rovnica hyperboly so stredom v bode S = [ x₀, y₀ ] a polosami dĺžok a, b má v prípade, ak je hlavná os v smere osi x tvar

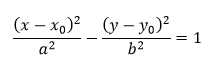
Ak je hlavná os v smere osi y rovnica tejto hyperboly nadobúda tvar

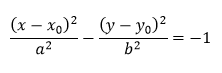
Rovnice priestorových útvarov

Rovnica priestorového útvaru je vo všeobecnosti rovnicou s tromi neznámymi x, y a z, ktorá rovnako ako rovnica rovinného útvaru určuje tento útvar na základe pravidla spomínaného v časti Základné pojmy. Poznáme rôzne druhy rovníc priestorových útvarov.

Normálová rovnica roviny

Podobným spôsobom, akým získavame normálovú rovnicu priamky v rovine dostávame aj normálovú rovnicu roviny určenej bodom X₀ a normálovým vektorom n, ktorá má tvar

Ak súradnice normálového vektora kolmého na túto rovinu sú n = [ a, b, c ] a určujúceho bodu P [ x₀, y₀, z₀ ], rozpísaním danej rovnice do súradníc dostávame

Ďalšou úpravou tejto rovnice získavame všeobecnú rovnicu roviny v priestore.

Všeobecná rovnica roviny a polpriestora

Všeobecná rovnica roviny je rovnica v tvare

Geometrický význam týchto čísel je podobný ako pri všeobecnej rovnici priamky v rovine. Čísla a, b, c sú súradnicami normálového vektora tejto roviny n [ a, b, c ] a číslo d je jeho skalárnym súčinom s polohovým vektorom ľubovoľného bodu roviny.

Polpriestory určené touto priamkou majú nerovnice

Každá rovina má v priestore nekonečne veľa všeobecných rovníc, ktoré sú nenulovým násobkom jednej z nich.

Parametrické rovnice priamky v priestore

Parametrické rovnice priamky v priestore sú podobné tým v rovine. Priamka určená bodom X₀ [x₀, y₀, z₀] a smerovým vektorom s [s₁, s₂, s₃] má vektorový tvar

Všeobecnú rovnicu priamka v priestore nemá vzhľadom na to, že smer jej normálového vektora nie je možné jednoznačne určiť.

Parametrické rovnice roviny

Ak poznáme niektorý bod roviny X₀ = [ x₀, y₀, z₀ ] a jej dva nerovnobežné smerové vektory r [ r₁, r₂, r₃ ] a s [s₁, s₂, s₃ ], tak ľubovoľný bod priestoru X [ x, y, z ] leží v tejto rovine práve vtedy, ak X - X₀ je lineárnou kombináciou vektorov r a s. To znamená, že existujú také parametre t, u ∈ R, že platí výraz

Parametrické rovnice danej roviny získame rozpísaním tejto rovnice do súradníc. Vznikajú tak rovnice v tvare

Každá rovina má nekonečne veľa parametrických vyjadrení. Práca s parametrickými rovnicami roviny je však vo väčšine prípadov pomerne komplikovaná, čo je dôvodom, prečo sa takéto rovnice prakticky takmer vôbec nevyužívajú.

Rovnica guľovej plochy

Pod pojmom guľová plocha chápeme množinu bodov priestoru, ktoré majú od daného pevného bodu S rovnakú vzdialenosť r nazývanú polomer. Guľová plocha so stredom S = [ x₀, y₀, z₀ ] a polomerom r je vyjadrovaná rovnicou

Úlohy

Príklad 1.
Na súradnicovej sústave roviny vyznačte 3 body, ktorých súradnice sú [0,0], [1,0.5] a [0.5,1].

Príklad 2.
Utvorte a znázornite množinu 15 bodov, ktorých x-ové súradnice sú čísla od 0 po 14, a y-ové súradnice sú náhodné čísla z intervalu (10,50).

Príklad 3.
Vynásobte vektor v = [3,2,1] konštantou c = 4.

Príklad 4.
Nech sú dané vektory u = [4,8,12] a v = [3,5,9]. Vypočítajte ich súčet, rozdiel (u - v) a skalárny súčin.

Príklad 5.
Vypočítajte vektorový súčin vektorov u = [1,2,3] a v = [3,2,1].

Príklad 6.
Znázornite 2 úsečky so spoločným bodom A, ktoré sú dané bodmi A[0.5,1], B[0,0] a A[0.5,1], C[1,0.5].

Príklad 7.
Vyznačne trojuholník definovaný spomínanými bodmi A[0.5,1], B[0,0], C[1,0.5].

Príklad 8.
Znázornite jednotkovú križnicu (kružnicu so stredom v počiatku súradnicovej sústavy s polomerom r = 1).

Príklad 9.
Znázornite elipsu a jej stred, ktorý je počiatkom súradnicovej sústavy, pričom dĺžka jej hlavnej poloosi a = 2 a dĺžka jej vedľajšej poloosi b = 1.

Príklad 10.
Vyznačte parabolu, danú napr. funkciou x².

Príklad 11.
Nech je v priestore daná úsečka AB, pričom A = [0,0,0] a B = [1,1,1]. Znázornite túto úsečku.

Príklad 12.
Znázornite v priestore rovinu danú rovnicou x = 1.

Príklad 13.
Znázornite rovnicu x + y + y = 1 v 3D.

Príklad 14.
Znázornite guľu v polomerom r = 1.

Príklad 15.
Zobrazte kužeľ s polomerom podstavy r = 0.5 a výškou v = 1.

Príklad 16.
Znázornite rez kužeľa s polomerom podstavy r = 0.5 a výškou v = 1 rovinou danou rovnicou x + y + z = 0.5.

SageMath Cell