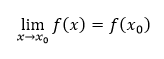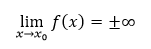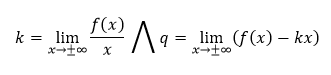Diferenciálny počet
Kľúčové slová:
diferenciálny počet, limity, vlastná limita vo vlastnom bode, nevlastná limita vo vlastnom bode, vlastná limita v nevlastnom bode, nevlastná limita v nevlastnom bode, jednostrnné limity, limita zľava, limita sprava, limita postupnosti, aritmetické pravidlá počítania limít, derivácia funkcie, geometrická definícia derivácie, druhy derivácií, vlastná derivácia, nevlastná derivácia, jednostranné derivácie, derivácia zľava, derivácia sprava, pravidlá derivovania, derivácie elementárnych funkcií, derivácie vyšších rádov, funkcia, priebeh funkcie, definičný obor, obor hodnôt, vlastnosti symetrie a periodicity, významné body, spojitosť funkcie, asymptoty grafu funkcie, monotónnosť funkcie, lokálne extrémy, konvexnosť a konkávnosť, inflexné body
Veľkou súčasťou technických vied je skúmanie a popisovanie javov a ich vzájomných závislostí. Cieľom skúmania určitého javu môže byť zistenie okamžitého stavu javu alebo jeho celkového priebehu.
Získavanie poznania o okamžitom stave javu na základe jeho priebehu je matematicky umožnené práve metódou nazývanou diferenciálny počet.
Základným pojmom diferenciálneho počtu, ale v podstate aj celej matematickej analýzy je tzv. derivácia. Derivácia je prostriedkom, ktorý meria zmenu hodnôt závislej veličiny vzhľadom k zmene hodnôt nezávislej veličiny.
K pochopeniu a správnemu použitiu derivácie je však potrebné najprv rozumieť pojmom ako funkcia, jej priebeh a limity funkcií.
Limity funkcie
Limita funkcie je hodnota, ku ktorej sa funkcia priblíži, keď sa vstupná premenná tejto funkcie priblíži k istej hodnote. Limity sa v matematickej analýze využívajú na definovanie derivácie a spojitosti.
Hovoríme, že funkcia f má v bode x0 limitu L, ak pre každé ε > 0 existuje také δ > 0, že pre každé x ∈ D(f), x ≠ x0 platí
ak | x - x0 | < δ, tak | f(x) - L | < ε
Limitu funkcie f označujeme ako
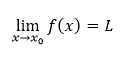
K tomu, aby mohla limita funkcie f v bode x0 existovať, nemusí byť v tomto bode definovaná.
Vlastná limita vo vlastnom bode
O limite funkcie f hovoríme, že je vlastnou limitou funkcie vo vlastnom bode, ak má v bode x0 ∈ R limitu L ∈ R.
Takéto limity označujeme ako
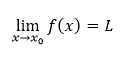
Nevlastná limita vo vlastnom bode
O limite funkcie f hovoríme, že je nevlastnou limitou funkcie vo vlastnom bode, ak má v bode x0 ∈ R limitu L = ±∞.
Tieto limity označujeme ako
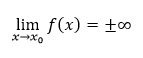
Vlastná limita v nevlastnom bode
Limite funkcie f hovoríme, že je vlastnou limitou funkcie v nevlastnom bode, ak má v bode x0 = ±∞ limitu L ∈ R.
Limity tohto druhu označujeme zápisom
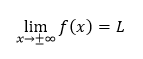
Nevlastná limita v nevlastnom bode
Limite funkcie f hovoríme, že je nevlastnou limitou funkcie v nevlastnom bode, ak má v bode x0 = ±∞ limitu L = ±∞.
Takéto limity označujeme zápisom
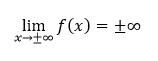
Jednostranné limity
V prípade, že pri definovaní limity funkcie f vo vlastnom bode x0 ∈ R vezmeme do úvahy iba body umiestnené po jednej jeho strane, hovoríme o jednostranných limitách. Za jednostranné limity funkcie považujeme limitu zľava a limitu sprava.
Funkcia f má v bode x0 limitu zľava L ∈ R, ak pre všetky x ∈ (x0 - δ, x0) platí
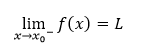
Funkcia f má v bode x0 limitu sprava L ∈ R, ak pre všetky x ∈ (x0, x0 + δ) platí
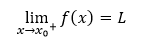
Existencia vlastnej limity funkcie f v bode x0 je podmienená existenciou spomínaných jednostranných limít danej funkcie, ktoré sa navzájom rovnajú. Toto pravidlo symbolicky vyjadrujeme zápisom
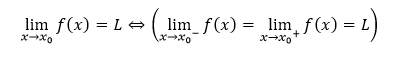
Limita postupnosti
Pod pojmom postupnosť rozumieme reálnu funkciu, ktorej D(f) = N.
Limity postupností počítame rovnako ako limity funkcií v nevlastnom bode. Riadime sa pritom pravidlom:
Nech f je taká funkcia, že pre každé n ∈ N platí f(n) = an a existuje limita
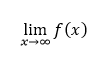
Potom existuje aj limita postupnosti, pre ktorú platí
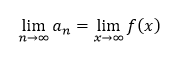
Aritmetické pravidlá pre počítanie limít
Pre počítanie s limitami platia určité pravidlá:

Derivácia funkcie
Pojem derivácia môžeme definovať z rôznych uhlov pohľadu. Všeobecne je jej účelom získať rýchlosť zmeny určitej meniacej sa veličiny. Pri derivácii funkcie f teda chceme určiť rýchlosť zmeny funkcie, konkrétne pomer zmeny f(x) voči zmene x.
Proces počítania derivácie určitej funkcie nazývame derivovanie.
Geometrická definícia a interpretácia derivácie
Určenie derivácie funkcie v grafickom znázornení znamená nájdenie sklonu krivky v danom bode funkcie. Tento sklon je daný uhlom, ktorý zviera dotyčnica k tejto krivke s osou x. Číselne túto veľkosť uhlu vyjadrujeme ako smernicu dotyčnice (tangens uhlu).
Majme danú funkciu f, ku ktorej hľadáme dotyčnicu, ak dotykovým bodom je bod T = [ x0, f(x0) ]. Smernicu kp priamky p (sečnice grafu) určenej ľubovoľným bodom grafu funkcie A = [ x1, f(x1) ] a bodom T môžeme vyjadriť vzťahom
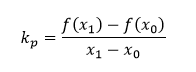
Potom smernicu kt hľadanej dotyčnice vypočítame vzťahom
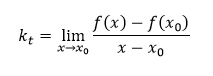
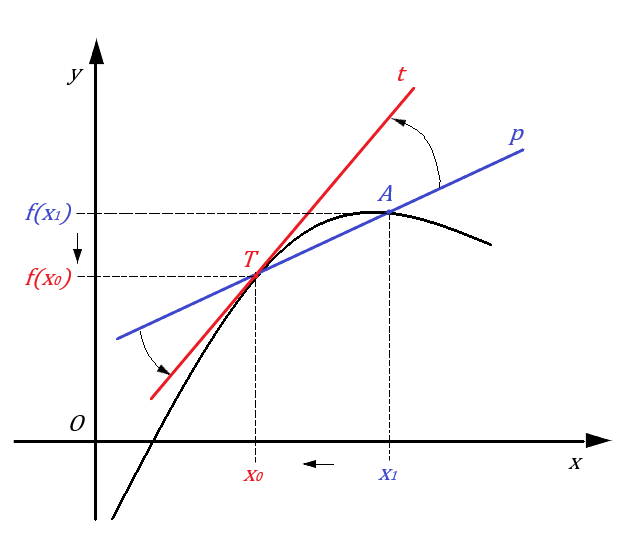
Ak takáto limita existuje a x0 ∈ D(f) nazývame ju derivácia funkcie f v bode x0 a označujeme ju zápisom
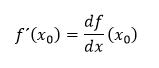
Druhy derivácií
Vzhľadom na to, akú má limita, ktorá je deriváciou funkcie vlastnosť rozoznávame viaceré druhy derivácií.
Nech má funkcia f v bode x0 ∈ D(f) limitu
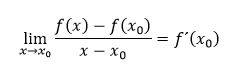
potom môžeme povedať, že funkcia f má v bode x0:
- vlastnú deriváciu, ak f´(x0) ∈ R
- nevlastnú deriváciu, ak f´(x0) = ±∞
Pokiaľ je táto limita jednostranná, tak deriváciu funkcie f v bode x0 nazývame:
- derivácia zľava, ak ide o limitu
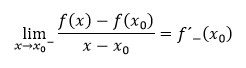
- derivácia sprava, ak ide o limitu
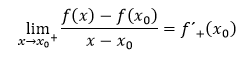
Rovnako, ako pre limitu aj pre deriváciu platí podmienka, že derivácia funkcie f v bode x0 existuje, iba ak existujú obe jednostranné derivácie funkcie f v bode x0, ktoré sú navzájom rovné a platí

Pravidlá derivovania
Podobne ako pre vektory, matice a limity aj pre derivácie funkcií vzniknutých algebrickými operáciami viacerých funkcií existujú určité pravidlá, podľa ktorých ich počítame.
Nech sú dané funkcie f a g, ktoré majú v bode x0 ∈ R deriváciu a nech c ∈ R je ľubovoľná konštanta. Potom platia tieto pravidlá:
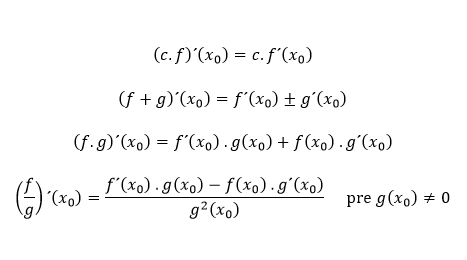
Okrem týchto pravidiel poznáme aj tzv. reťazové pravidlo, ktoré vraví o derivácii zloženej funkcie, ktorej vnútorná zložka je ľubovoľná hladká funkcia.
Pod pojmom hladká funkcia na množine M rozumieme funkciu, ktorá má v každom bode x0 ∈ M ⊂ D(f) vlastnú deriváciu.
Uvažujme o zloženej funkcii F(x) = f(g(x)), pričom funkcie f a g sú hladké na svojich definičných oboroch a D(f) ⊇ H(g). Potom má aj zložená funkcia F(x) deriváciu v každom bode svojho definičného oboru a platí
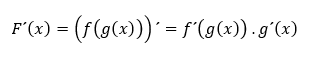
Derivácie elementárnych funkcií
Okrem pravidiel derivovania je k správnemu využitiu derivácie v praxi užitočné poznať a zapamätať si aj derivácie elementárnych funkcií. V nasledujúcich tabuľkách sa okrem premennej x objavujú aj čísla a, b, c ∈ R, ktoré sú konštanty a n ∈ N.





Derivácie vyšších rádov
Okrem opisovanej prvej derivácie existujú aj tzv. derivácie vyšších rádov. Istú funkciu alebo výraz totiž môžeme derivovať viackrát než len raz, vzhľadom na to, že aj derivácia funkcie je funkciou.
Ak je to možné tak funkciu f´, ktorá je deriváciou pôvodnej funkcie f môžeme tiež derivovať, čím vzniká tzv. derivácia druhého rádu (f´)´ tiež označovaná ako f´´.
Ako už bolo povedané, ak je to možné, tak funkciu môžeme derivovať viackrát než len raz, no dokonca aj viac než dvakrát. Preto zavádzame pojem derivácie n-tého rádu.
Nech n ∈ N. Potom n-tou deriváciou, alebo aj deriváciou n-tého rádu je funkcia, ktorú označujeme ako f (n) a definujeme ju rovnosťou
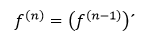
pričom
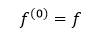
Pri deriváciách druhého a tretieho rádu sa často stretávame skôr so zápisom f´´ a f´´´ než s označením f (2) a f (3).
Počítanie derivácie funkcie vyššieho rádu nie je ničím špeciálne, ani zložité. Jedná sa len o opätovné derivovanie novovzniknutej funkcie. Z toho vyplýva, že pokiaľ chceme získať napr. deriváciu funkcie 3-tieho rádu, musíme funkciu f derivovať, potom derivovať výslednú funkciu f´, čím získame f´´, ktorú následne tiež derivujeme.
Funkcia a jej priebeh
V celej tejto časti nazvanej Diferenciálny počet sme rozprávali o funkciách. Preto je vhodné si pripomenúť, čo pojem funkcia a jej priebeh v matematike vlastne predstavujú.
Nech X a Y sú neprázdne číselné množiny a f:X→Y je zobrazenie množiny X do množiny Y. Presnejšie povedané, ak každý prvok x ∈ X jednoznačne určuje hodnotu prvku y ∈ Y tak, že platí f(x) = y, hovoríme o funkčnej závislosti alebo inak povedané aj funkcii.
Veličinu x nazývame nezávislou premennou a veličinu y naopak závislou premennou.
Popis priebehu funkcie tkvie v určení jej vlastností a načrtnutí jej grafu. Tento postup by mal pozostávať z určenia:
- definičného oboru funkcie a oboru hodnôt
- vlastnosti symetrie a periodicity
- významných bodov
- asymptôt grafu funkcie
- intervalov monotónnosti funkcie a jej lokálnych extrémov
- intervalov, kde je funkcia konvexná, konkávna a jej inflexných bodov
- náčrtu grafu funkcie
Definičný obor a obor hodnôt
Definičný obor funkcie f je spomínaná množina X všetkých nezávislých premenných, ktoré definujú funkciu. Označujeme ho symbolom D(f).
Obor hodnôt funkcie f označovaný ako H(f) predstavuje množinu všetkých hodnôt f(x), kde x ∈ D(f) a platí f(x) = y.
_H(f).png)
Vzhľadom na obor hodnôt funkcie môžeme určiť aj jej ohraničenosť. Funkcia f je
- zhora ohraničená, ak je zhora ohraničený jej obor hodnôt
- zdola ohraničená, ak je zdola ohraničený jej obor hodnôt
- ohraničená, ak je ohraničená zhora aj zdola (ak je ohraničený jej obor hodnôt)
Vlastnosti symetrie a periodicity
Pod určením vlastností symetrie a periodicity funkcie rozumieme určenie toho, či je skúmaná funkcia párna alebo nepárna a toho, či je periodická.
Funkcia f sa nazýva:
- párna, ak pre každé x ∈ X platí f(x) = f(-x)
- nepárna, ak pre každé x ∈ X platí - f(x) = f(-x)
- periodická, ak existuje λ > 0 také, že f(x) = f(x + λ) pre každé x ∈ X, pričom najmenšie číslo λ > 0, pre ktoré platí daná vlastnosť sa nazýva perióda funkcie
Vzhľadom na to, že párna funkcia priraďuje opačným číslam rovnaké hodnoty, graf takejto funkcie je súmerný podľa osi y. Naopak nepárna funkcia priraďuje opačným číslam opačné hodnoty a jej graf je súmerný podľa začiatku súradnicovej sústavy O [ 0, 0 ]. Definičné obory oboch z týchto funkcií sú symetrické množiny okolo bodu 0.
Nie každá funkcia však musí byť párna, nepárna, či periodická. Existujú aj funkcie, ktorým ani jednu z týchto vlastností pripísať nemôžeme.
Významné body a spojitosť funkcie
Významnými bodmi funkcie, ktoré môžeme pri popise jej priebehu určiť sú napr.: nulový bod funkcie, body spojitosti a nespojitosti, body, v ktorých je derivácia nespojitá či dokonca neexistuje a pod.
Nulový bod funkcie je bod x, v ktorom f(x) = 0.
Bodmi spojitosti sú čísla z definičného oboru, v ktorých je funkcia spojitá.
Naopak body nespojitosti sú čísla z definičného oboru, v ktorých funkcia spojitá nie je.
Spojitosť
Pod spojitosťou funkcie f rozumieme lokálnu vlastnosť, ktorá vraví, že pre všetky x ∈ D(f), ktoré sú v blízkosti bodu x0 ∈ D(f), sú aj funkčné hodnoty f(x) blízke hodnote f(x0). Symbolicky túto definíciu vyjadrujeme zápisom
ak | x - x0 | < δ, potom | f(x) - f(x0) | < ε
Ak je funkcia f spojitá v bode x0, potom existuje
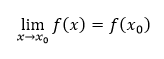
Asymptoty grafu funkcie
Asymptota grafu funkcie je priamka, ku ktorej sa graf funkcie v ∞ neobmedzene približuje. Môžeme ich určiť iba pri nespojitých funkciách.
Poznáme vertikálnu asymptotu (asymptotu bez smernice) a horizontálnu asymptoty (asymptoty so smernicou).
Hovoríme, že priamka x = x0 je vertikálnou asymptotou funkcie f v bode x0, ak má funkcia f v tomto bode aspoň jednu jednostrannú nevlastnú limitu
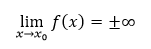
Hovoríme, že priamka y = kx + q je horizontálnou asymptotou funkcie f v ±∞ ak
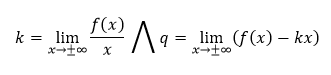
Monotónnosť funkcie a jej lokálne extrémy
Určenie monotónnosti funkcie spočíva v určení toho či funkčné hodnoty f(x) s rastúcou hodnotou x ∈ D(f) rastú, klesajú alebo ostávajú rovnaké a na akom intervale.
O funkcii f môžeme povedať, že je na množine M ⊂ D(f):
- rýdzo rastúca (rastúca), ak pre každé (x1 < x2) ∈ M platí f(x1) < f(x2)
- nerýdzo rastúca (neklesajúca), ak pre každé (x1 < x2) ∈ M platí f(x1) ≤ f(x2)
- rýdzo klesajúca (klesajúca), ak pre každé (x1 < x2) ∈ M platí f(x1) > f(x2)
- nerýdzo klesajúca (nerastúca), ak pre každé (x1 < x2) ∈ M platí f(x1) ≥ f(x2)
- monotónna, ak je neklesajúca alebo nerastúca
- rýdzo monotónna, ak je rýdzo rastúca alebo rýdzo klesajúca (môžeme o nej povedať aj to, že je prostá)
Lokálne extrémy funkcie sú body, v ktorých sa funkcia mení z klesajúcej na rastúcu a naopak. Takýmito bodmi môžu byť lokálne maximum alebo lokálne minimum. Funkcia f môže mať nekonečne veľa lokálnych miním a maxím.
Monotónnosť funkcie je možné určiť práve pomocou derivácie, ktorá je hlavným zameraním tejto podkapitoly. Zo samotnej definície derivácie vyplýva veta:
Nech funkcia f je „hladká“ na intervale (a,b), potom je na tomto intervale:
- rýdzo rastúca, ak pre každé x ∈ (a,b) je f´(x) > 0
- rýdzo klesajúca, ak pre každé x ∈ (a,b) je f´(x) < 0
Ak funkcia f, ktorá je hladká na intervale (a,b) má lokálny extrém v bode (x0, f(x0)) pre každé x0 ∈ (a,b), tak f´(x0) = 0. K nájdeniu lokálnych extrémov funkcie teda musíme nájsť body x0 ∈ D(f), pre ktoré je f´(x0) = 0 alebo takáto derivácia neexistuje.
Tieto body nazývame aj stacionárne body. Nie všetky stacionárne body funkcie však musia byť lokálnym maximom alebo minimom. Záleží na tom či je funkcia v okolí tohto bodu rastúca či klesajúca, a z ktorej strany.
K určeniu toho, či je nájdený lokálny extrém minimom alebo maximom môžeme využiť druhú deriváciu funkcie v tomto bode. Potom platí, že funkcia má v bode x0:
- lokálne maximum, ak f´´(x) < 0
- lokálne minimum, ak f´´(x) > 0
Konvexnosť a konkávnosť funkcie
O funkcii f hovoríme, že je konvexná v intervale (a,b), ak jej graf leží nad každou k nej zostrojenou dotyčnicou. Naopak môžeme o funkcii f povedať, že je konkávna v intervale (a,b), ak jej graf leží pod každou k nej zostrojenou dotyčnicou.
Konvexnosť a konkávnosť funkcie je možné určiť aj pomocou jej druhej derivácie.
Nech funkcia f má druhú deriváciu na intervale (a,b), potom o nej môžeme povedať, že je na tomto intervale:
- konvexná, ak pre každé x ∈ (a,b) je f´´(x) > 0
- konkávna, ak pre každé x ∈ (a,b) je f´´(x) < 0
Bod, v ktorom sa funkcia mení z konvexnej na konkávnu a naopak sa nazýva inflexný bod.
Ak je bod x0 ∈ (a,b) jediný bod, pre ktorý je f´´(x0) = 0, a ak existujú x1, x2 ∈ (a,b), pre ktoré f´´(x1) > 0 a f´´(x2) < 0, potom je práve bod (x0, f(x0)) inflexným bodom tejto funkcie f.
Úlohy
Príklad 1.
Zistite, či má funkcia 1/x^2 v bode x → 0 vlastnú alebo nevlastnú limitu. V oboch prípadoch uveďte aj jej presnú hodnotu.
Riešenie v SageMath
Príklad 2.
Vypočítajte limitu ľubovoľnej funkcie, napr.: 6x + 2 v ľubovoľnom bode, napr.: x → 10.
Riešenie v SageMath
Príklad 3.
Nech je daná funkcia f(x), napr.: f(x) = sin(x). K tejto funkcii existuje v dotykovom bode T = [x0, f(x0)] dotyčnica t.
Určte a graficky znázornite dotykový bod T a dotyčnicu t k danej funkcii f(x), ak je bod x0 rovný napr. hodnote π/4.
Riešenie v SageMath
Modifikácia úlohy z knihy:
RAZVAN, A. MEZEI.: An Introduction to Sage Programming – With Applications to SAGE Interacts for Numerical Methods. New Jersey, USA. John Wiley & Sons, Inc., 2016. 245 s. ISBN 9781119122784
Príklad 4.
Nájdite prvú deriváciu ľubovoľnej funkcie, napr.: 2.tan(x).
Riešenie v SageMath
Príklad 5.
Nech je daná funkcia f(x), napr.: f(x) = x2. Nájdite k tejto funkcii deriváciu. Následne nakreslite obe z týchto funkcií v rámci jedného súradnicového systému.
Riešenie v SageMath
Príklad 6.
Počítajte derivácie vyššieho rádu ľubovoľnej funkcie. Napríklad deriváciu 2. rádu funkcie 2x3 - x2 + 3x
Riešenie v SageMath
Príklad 7.
Zistite, či je funkcia 1/(x3 - x) v bode x = 3 spojitá.
Riešenie v SageMath
V skutočnosti zaznamená SageMath v prípade, že je funkcia v danom bode nespojitá chybu a vypíše hlásenie, že dochádza k deleniu 0.
Príklad 8.
Zobrazením grafu a asymptôt funkcie 1/(x3 - x) na intervale, ktorý zahŕňa číslo 3 sa presvedčte, či platí tvrdenie z predchádzajúcej úlohy.
Riešenie v SageMath
Príklad 9.
Nájdite asymptoty grafu ľubovoľnej funkcie napr.: tan(x) na ľubovoľnom intervale 〈a,b〉.
Riešenie v SageMath
SageMath Cell
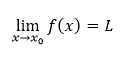
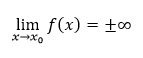
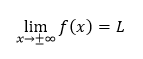
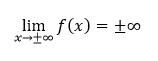
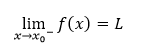
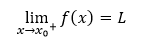
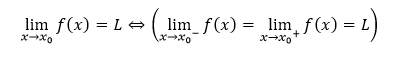
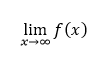
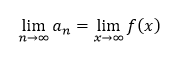

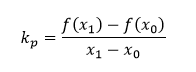
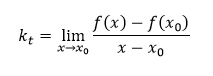

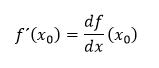
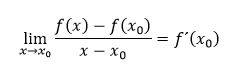
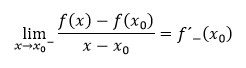
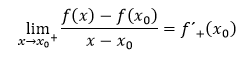

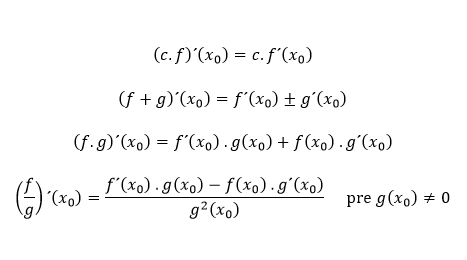
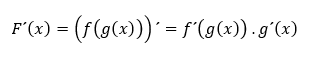





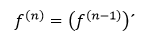
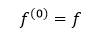
_H(f).png)